题目内容
2.在区域{0≤x≤10≤y≤1内任意取一点P(x,y),则x2+y2>1的概率是( )| A. | 2π−44 | B. | π−24 | C. | π4 | D. | 4−π4 |
分析 根据几何概型的概率公式分别计算出对应区域的面积,代入几何概率公式可求.
解答 解:由题意可得,区域{0≤x≤10≤y≤1表示的是以1为边长的正方形ABCD,其面积为1
x2+y2>1的区域为正方形内单位圆外的部分,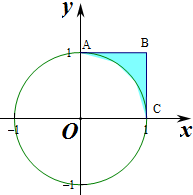
则阴影部分的面积S=1-14×π×12=1-π4,
则对应的概率P=1−π41=4−π4,
故选:D
点评 本题主要考查几何概型的概率计算,根据条件求出对应区域的面积是解决本题的关键.

练习册系列答案
相关题目
17.定义:如果函数f(x)在[a,b]上存在x1,x2 (a<x1<x2<b),满足f′(x1)=f(b)−f(a)b−a,f′(x2)=f′(b)−f′(a)b−a,则称数x1,x2 为[a,b]上的“对望数”函数f(x)为[a,b]上的“对望函数”,已知函数f(x)=13x3−x2+m是[0,m]上的“对望函数”,则实数m的取值范围是( )
| A. | (1,32) | B. | (1,32)∪(32,3) | C. | (2,3) | D. | (32,3) |
7.已知命题p:若→a是非零向量,λ是非零实数,则→a与-λ→a方向相反;命题q:|-λ→a|=|λ|•→a.则下列命题为真命题的是( )
| A. | p∧q | B. | p∨q | C. | (¬p)∨q | D. | p∧(¬q) |
11.运行如下程序框图,如果输入的x∈(-∞,1],则输出的y属于( )
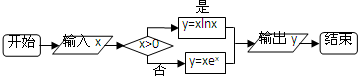

| A. | [-1e,0] | B. | [-1e,0) | C. | [-1e,+∞) | D. | [-1e,e) |
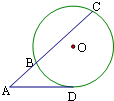 如图,从圆O外一点A引圆的切线AD和割线ABC,已知AD=2
如图,从圆O外一点A引圆的切线AD和割线ABC,已知AD=2