题目内容
【题目】已知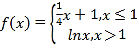 ,则方程
,则方程![]() 恰有2个不同的实根,实数
恰有2个不同的实根,实数![]() 取值范围__________________.
取值范围__________________.
【答案】![]()
【解析】
将问题转化为当直线![]() 与函数
与函数![]() 的图象有
的图象有![]() 个交点时,求实数
个交点时,求实数![]() 的取值范围,并作出函数
的取值范围,并作出函数![]() 的图象,考查当直线
的图象,考查当直线![]() 与曲线
与曲线![]() 相切以及直线
相切以及直线![]() 与直线
与直线![]() 平行这两种临界位置情况,结合斜率的变化得出实数
平行这两种临界位置情况,结合斜率的变化得出实数![]() 的取值范围。
的取值范围。
问题等价于当直线![]() 与函数
与函数![]() 的图象有
的图象有![]() 个交点时,求实数
个交点时,求实数![]() 的取值范围。
的取值范围。
作出函数![]() 的图象如下图所示:
的图象如下图所示:
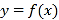
先考虑直线![]() 与曲线
与曲线![]() 相切时,
相切时,![]() 的取值,
的取值,
设切点为![]() ,对函数
,对函数![]() 求导得
求导得![]() ,切线方程为
,切线方程为![]() ,
,
即![]() ,则有
,则有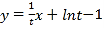 ,解得
,解得![]() .
.
由图象可知,当![]() 时,直线
时,直线![]() 与函数
与函数![]() 在
在![]() 上的图象没有公共点,在
上的图象没有公共点,在![]() 有一个公共点,不合乎题意;
有一个公共点,不合乎题意;
当![]() 时,直线
时,直线![]() 与函数
与函数![]() 在
在![]() 上的图象没有公共点,在
上的图象没有公共点,在![]() 有两个公共点,合乎题意;
有两个公共点,合乎题意;
当![]() 时,直线
时,直线![]() 与函数
与函数![]() 在
在![]() 上的图象只有一个公共点,在
上的图象只有一个公共点,在![]() 有两个公共点,不合乎题意;
有两个公共点,不合乎题意;
当![]() 时,直线
时,直线![]() 与函数
与函数![]() 在
在![]() 上的图象只有一个公共点,在
上的图象只有一个公共点,在![]() 没有公共点,不合乎题意.
没有公共点,不合乎题意.
综上所述,实数![]() 的取值范围是
的取值范围是![]() ,故答案为:
,故答案为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】体育测试成绩分为四个等级:优、良、中、不及格.某班50名学生参加测试结果如下:
等级 | 优(86~100分) | 良(75~85分) | 中(60~74分) | 不及格(1~59分) |
人数 | 5 | 21 | 22 | 2 |
(1)估计该班学生体育测试的平均成绩;
(2)从该班任意抽取1名学生,求这名学生的测试成绩为“优”或“良”的概率.
