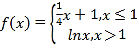题目内容
【题目】抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 的直线交抛物线于
的直线交抛物线于![]() ,
,![]() 两点.
两点.
(1)![]() 为坐标原点,求证:
为坐标原点,求证:![]() ;
;
(2)设点![]() 在线段
在线段![]() 上运动,原点
上运动,原点![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,求四边形
,求四边形![]() 面积的最小值
面积的最小值
【答案】(Ⅰ)见解析;(Ⅱ)![]() 时,四边形
时,四边形![]() 的面积最小,最小值是
的面积最小,最小值是![]() .
.
【解析】
试题(1)先利用已知条件设出直线AB的方程,与抛物线联立方程组,然后结合韦达定理表示出向量的数量积,进而证明。
(2)根据由点![]() 与原点
与原点![]() 关于点
关于点![]() 对称,得
对称,得![]() 是线段
是线段![]() 的中点,从而点
的中点,从而点![]() 与点
与点![]() 到直线
到直线![]() 的距离相等,得到四边形
的距离相等,得到四边形![]() 的面积等于
的面积等于![]() ,结合三角形面积公式得到。
,结合三角形面积公式得到。
(Ⅰ)解:依题意![]() ,设直线
,设直线![]() 方程为
方程为![]() . …………1分
. …………1分
将直线![]() 的方程与抛物线的方程联立,消去
的方程与抛物线的方程联立,消去![]() 得
得![]() .……3分
.……3分
设![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
![]() =1,
=1,
故![]() .………………6分
.………………6分
(Ⅱ)解:由点![]() 与原点
与原点![]() 关于点
关于点![]() 对称,得
对称,得![]() 是线段
是线段![]() 的中点,从而点
的中点,从而点![]() 与点
与点![]() 到直线
到直线![]() 的距离相等,所以四边形
的距离相等,所以四边形![]() 的面积等于
的面积等于![]() .……8分
.……8分
因为![]() ……………9分
……………9分
![]() ,…………11分
,…………11分
所以![]() 时,四边形
时,四边形![]() 的面积最小,最小值是
的面积最小,最小值是![]() . ……12分
. ……12分

【题目】科学研究表明:人类对声音有不的感觉,这与声音的强度![]() 单位:瓦
单位:瓦![]() 平方米
平方米![]() 有关
有关![]() 在实际测量时,常用
在实际测量时,常用![]() 单位:分贝
单位:分贝![]() 来表示声音强弱的等级,它与声音的强度I满足关系式:
来表示声音强弱的等级,它与声音的强度I满足关系式:![]() 是常数
是常数![]() ,其中
,其中![]() 瓦
瓦![]() 平方米
平方米![]() 如风吹落叶沙沙声的强度
如风吹落叶沙沙声的强度![]() 瓦
瓦![]() 平方米,它的强弱等级
平方米,它的强弱等级![]() 分贝.
分贝.
![]() 已知生活中几种声音的强度如表:
已知生活中几种声音的强度如表:
声音来源
声音大小 | 风吹落叶沙沙声 | 轻声耳语 | 很嘈杂的马路 |
强度 |
|
|
|
强弱等级 | 10 | m | 90 |
求a和m的值
![]() 为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.
为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.
【题目】一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
转速x(转/秒) | 2 | 4 | 5 | 6 | 8 |
每小时生产有缺点的零件数y(件) | 30 | 40 | 60 | 50 | 70 |
(1)画散点图;
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为89个,那么机器的运转速度应控制在什么范围内?(参考数值:![]() )
)