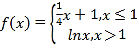题目内容
【题目】已知函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若![]() 恒成立,则称
恒成立,则称![]() 为
为![]() 的一个上界函数,当(1)中的
的一个上界函数,当(1)中的![]() 为函数
为函数![]() 的一个上界函数时,求
的一个上界函数时,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,对(1)中的
时,对(1)中的![]() ,讨论
,讨论![]() 在区间
在区间![]() 上极值点的个数.
上极值点的个数.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)在
;(3)在![]() 上,当
上,当![]() 时,
时,![]() 无极值点;当
无极值点;当![]() 或者
或者![]() 时,
时,![]() 有1个极值点.;当
有1个极值点.;当![]() 且
且![]() 时,
时,![]() 有2个极值点.
有2个极值点.
【解析】
试题(1)求导,根据导数的几何意义![]() ,由题意知
,由题意知![]() ,解方程组可得
,解方程组可得![]() 的值.(2)问题等价于
的值.(2)问题等价于![]() 恒成立,再转化为
恒成立,再转化为![]() 对
对![]() 恒成立.命名新函数令
恒成立.命名新函数令![]() 求导,讨论导数的正负,得函数的单调区间,根据函数的单调性求其最值.令其最小值大于等于0即可.(3)求导,讨论导数的正负得函数的单调区间.根据单调性求其最值.讨论最值与0的大小,结合函数图像判断零点个数.
求导,讨论导数的正负,得函数的单调区间,根据函数的单调性求其最值.令其最小值大于等于0即可.(3)求导,讨论导数的正负得函数的单调区间.根据单调性求其最值.讨论最值与0的大小,结合函数图像判断零点个数.
试题解析:(1)![]() ,由已知
,由已知![]() 解得
解得![]()
(2)![]() 恒成立
恒成立![]() 对
对![]() 恒成立.
恒成立.
令![]() 则
则![]() ,当
,当![]() )时,
)时,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 单调递减,
单调递减,![]() ,故
,故![]() .
.
(3)由(1)知![]()
![]()
![]() ,
,![]() 的解为
的解为![]() .
.
①当![]() 时,
时,![]()
![]() 在(0,2)上单调递增,无极值点;
在(0,2)上单调递增,无极值点;
②当 且
且![]() ,即
,即![]() 且
且![]() 时,
时,![]() 有2个极值点;
有2个极值点;
③当 或
或 ,即
,即![]() 或者
或者![]() 时,
时,![]() 有1个极值点.
有1个极值点.
综上知,在![]() 上,当
上,当![]() 时,
时,![]() 无极值点;当
无极值点;当![]() 或者
或者![]() 时,
时,![]() 有1个极值点;当
有1个极值点;当![]() 且
且![]() 时,
时,![]() 有2个极值点.
有2个极值点.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列出了如表并给出了部分数据:
在某一个周期内的图象时,列出了如表并给出了部分数据:
| 0 |
| π |
|
|
x |
|
| |||
| 0 | 2 | 0 | 0 |
(1)请根据上表数据,写出函数![]() 的解析式;(直接写出结果即可)
的解析式;(直接写出结果即可)
(2)求函数![]() 的单调递增区间;
的单调递增区间;
(3)设![]() ,已知函数
,已知函数![]() 在区间
在区间![]() 上的最大值是img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/26/20/139c9676/SYS202011262014544768390673_ST/SYS202011262014544768390673_ST.013.png" width="24" height="24" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,求t的值以及函数
上的最大值是img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/26/20/139c9676/SYS202011262014544768390673_ST/SYS202011262014544768390673_ST.013.png" width="24" height="24" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,求t的值以及函数![]() 在区间[
在区间[![]() 上的最小值.
上的最小值.
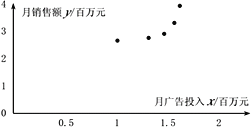
【题目】长沙某公司对其主推产品在过去5个月的月广告投入xi(百万元)和相应的销售额yi(百万元)进行了统计,其中i=1,2,3,4,5,对所得数据进行整理,绘制散点图并计算出一些统计量如下:
|
|
|
|
|
|
|
68 | 10.3 | 15.8 | -192.12 | 1.602 | 0.46 | 3.56 |
其中![]() ,i=1,2,3,4,5.
,i=1,2,3,4,5.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为月销售额关于月广告投入xi的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为月销售额关于月广告投入xi的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及题中所给数据,建立y关于x的回归方程,并据此估计月广告投入200万元时的月销售额.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: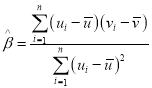 ,
,![]() .
.