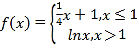题目内容
【题目】已知△ABC的三个内角A,B,C对应的边长分别为a,b,c,向量m=(sinB,1﹣cosB)与向量n=(2,0)的夹角θ的余弦值为![]() .
.
(1)求角B的大小;
(2)若b=![]() ,求a+c的取值范围.
,求a+c的取值范围.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)由向量m=(sinB,1-cosB),向量n=(2,0)可求得cosθ=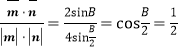 ,即可求角B的大小;
,即可求角B的大小;
(2)由余弦定理,得b2=a2+c2-2accos![]() π=a2+c2+ac,结合重要不等式可知b2=(a+c)2-ac≥(a+c)2-
π=a2+c2+ac,结合重要不等式可知b2=(a+c)2-ac≥(a+c)2-![]() =
=![]() (a+c)2,给出b=
(a+c)2,给出b=![]() 即可求得a+c的取值范围.
即可求得a+c的取值范围.
(1)∵m=(sinB,1-cosB),n=(2,0),∴m·n=2sinB,
|m|=![]()
![]() .
.
∵0<B<π,∴0<![]() <
<![]() .∴sin
.∴sin![]() >0.
>0.
∴|m|=2sin![]() .
.
又∵|n|=2,
∴cosθ=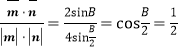 .
.
∴![]() ,∴B=
,∴B=![]() .
.
(2)由余弦定理,得b2=a2+c2-2accos![]() π=a2+c2+ac=(a+c)2-ac≥(a+c)2-
π=a2+c2+ac=(a+c)2-ac≥(a+c)2-![]() =
=![]() (a+c)2,当且仅当a=c时,取等号.∴(a+c)2≤4,即a+c≤2.
(a+c)2,当且仅当a=c时,取等号.∴(a+c)2≤4,即a+c≤2.
又a+c>b=![]() ,∴a+c∈(
,∴a+c∈(![]() ,2].
,2].

【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列出了如表并给出了部分数据:
在某一个周期内的图象时,列出了如表并给出了部分数据:
| 0 |
| π |
|
|
x |
|
| |||
| 0 | 2 | 0 | 0 |
(1)请根据上表数据,写出函数![]() 的解析式;(直接写出结果即可)
的解析式;(直接写出结果即可)
(2)求函数![]() 的单调递增区间;
的单调递增区间;
(3)设![]() ,已知函数
,已知函数![]() 在区间
在区间![]() 上的最大值是img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/26/20/139c9676/SYS202011262014544768390673_ST/SYS202011262014544768390673_ST.013.png" width="24" height="24" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,求t的值以及函数
上的最大值是img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/26/20/139c9676/SYS202011262014544768390673_ST/SYS202011262014544768390673_ST.013.png" width="24" height="24" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,求t的值以及函数![]() 在区间[
在区间[![]() 上的最小值.
上的最小值.