题目内容
(本小题满分14分) 已知函数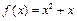 及正整数数列
及正整数数列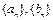 . 若
. 若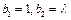 ,且当
,且当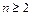 时,有
时,有 ; 又
; 又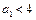 ,
,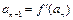 ,且
,且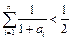 对任意
对任意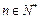 恒成立. 数列
恒成立. 数列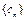 满足:
满足: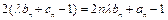 .
.
(1) 求数列 及
及 的通项公式;
的通项公式;
(2) 求数列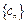 的前
的前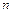 项和
项和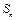 ;
;
(3) 证明存在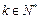 ,使得
,使得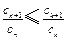 对任意
对任意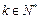 均成立.
均成立.
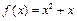 及正整数数列
及正整数数列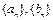 . 若
. 若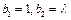 ,且当
,且当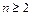 时,有
时,有 ; 又
; 又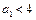 ,
,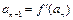 ,且
,且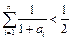 对任意
对任意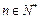 恒成立. 数列
恒成立. 数列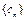 满足:
满足: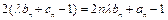 .
.(1) 求数列
 及
及 的通项公式;
的通项公式;(2) 求数列
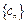 的前
的前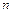 项和
项和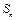 ;
;(3) 证明存在
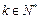 ,使得
,使得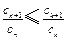 对任意
对任意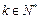 均成立.
均成立.(1)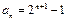 ,
,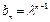 , (2) 当
, (2) 当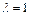 时,
时, .这时数列
.这时数列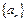 的前
的前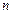 项和
项和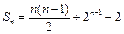 , (3) 存在
, (3) 存在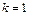 ,使得
,使得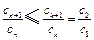 对任意
对任意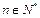 均成立
均成立
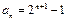 ,
,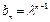 , (2) 当
, (2) 当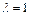 时,
时, .这时数列
.这时数列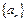 的前
的前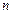 项和
项和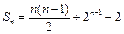 , (3) 存在
, (3) 存在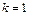 ,使得
,使得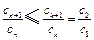 对任意
对任意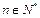 均成立
均成立(1) 由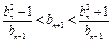 得:
得: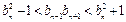 .因为
.因为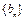 是正整数列,所以
是正整数列,所以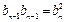 .于是
.于是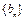 是等比数列. 又,
是等比数列. 又,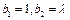 , 所以
, 所以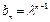 .
.
因为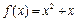 ,所以
,所以 ,于是:
,于是: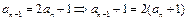 ,说明
,说明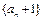 是以2为公比的等比数列. 所以
是以2为公比的等比数列. 所以
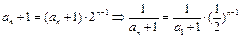
因为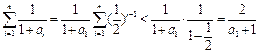 , 由题设知:
, 由题设知: 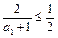 ,解得:
,解得: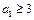 。
。
又因为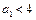 且
且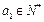 ,所以
,所以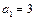 。
。
于是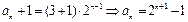 。
。
(2) 由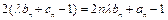 得:
得: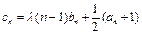 .由
.由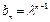 及
及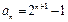 得:
得: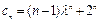
设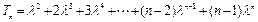 ①
①
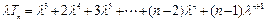 ②
②
当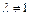 时,①式减去②式, 得
时,①式减去②式, 得
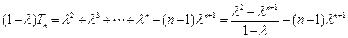
于是,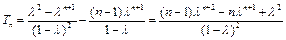
这时数列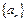 的前
的前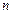 项和
项和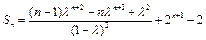 .
.
当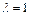 时,
时, .这时数列
.这时数列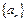 的前
的前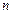 项和
项和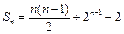 .
.
(3) 证明:通过分析,推测数列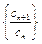 的第一项
的第一项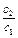 最大,下面证明:
最大,下面证明:
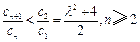 ③
③
由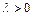 知
知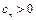 ,要使③式成立,只要
,要使③式成立,只要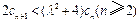 ,
,
因为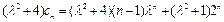
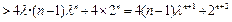
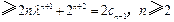 .
.
所以③式成立.
因此,存在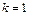 ,使得
,使得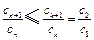 对任意
对任意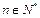 均成立.
均成立.
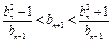 得:
得: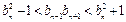 .因为
.因为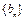 是正整数列,所以
是正整数列,所以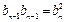 .于是
.于是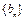 是等比数列. 又,
是等比数列. 又,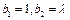 , 所以
, 所以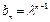 .
. 因为
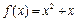 ,所以
,所以 ,于是:
,于是: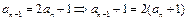 ,说明
,说明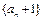 是以2为公比的等比数列. 所以
是以2为公比的等比数列. 所以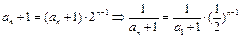
因为
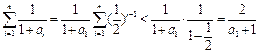 , 由题设知:
, 由题设知: 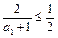 ,解得:
,解得: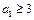 。
。又因为
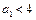 且
且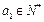 ,所以
,所以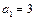 。
。于是
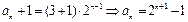 。
。(2) 由
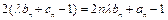 得:
得: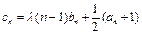 .由
.由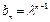 及
及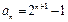 得:
得: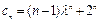
设
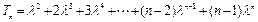 ①
①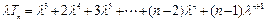 ②
②当
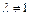 时,①式减去②式, 得
时,①式减去②式, 得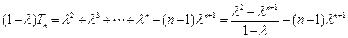
于是,
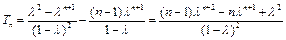
这时数列
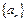 的前
的前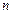 项和
项和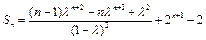 .
.当
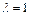 时,
时, .这时数列
.这时数列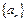 的前
的前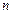 项和
项和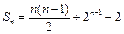 .
.(3) 证明:通过分析,推测数列
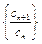 的第一项
的第一项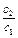 最大,下面证明:
最大,下面证明: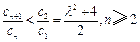 ③
③由
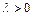 知
知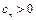 ,要使③式成立,只要
,要使③式成立,只要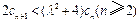 ,
,因为
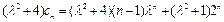
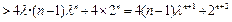
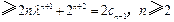 .
.所以③式成立.
因此,存在
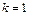 ,使得
,使得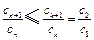 对任意
对任意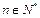 均成立.
均成立.
练习册系列答案
相关题目
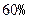 (即衰变了
(即衰变了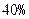 ),该动物大约在距今多少年前死亡?
),该动物大约在距今多少年前死亡?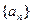 的前
的前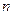 项和为
项和为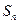 ,且满足
,且满足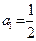 ,
,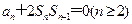 .(1)问:数列
.(1)问:数列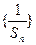 是否为等差数列?并证明你的结论;(2)求
是否为等差数列?并证明你的结论;(2)求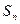 和
和 ;(3)求证:
;(3)求证: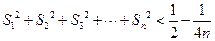 .
.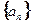 的前
的前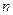 项和为
项和为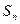 ,
,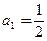 ,且
,且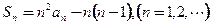
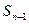 的递推关系式(
的递推关系式(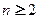 );
);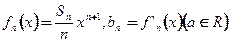 ,求数列
,求数列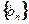 的前
的前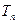 。
。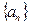 中前n项的和
中前n项的和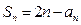 ,求数列的通项公式
,求数列的通项公式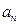 .
.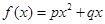 ,其中p>0,p+q>1。对于数列
,其中p>0,p+q>1。对于数列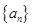 ,设它的前n项之和为
,设它的前n项之和为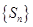 ,且
,且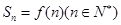 。
。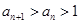 (3)证明:点
(3)证明:点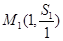 ,
,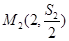 ,
,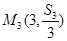 ,
, ,
,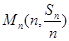 共线
共线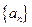 中,
中,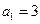 ,
,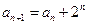 ,求
,求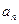 .
.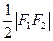 是
是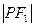 与
与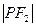 的等差中项,则动点P的轨迹是( ).
的等差中项,则动点P的轨迹是( ).