题目内容
(本小题满分12分)已知数列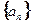 的前
的前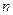 项和为
项和为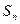 ,
,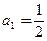 ,且
,且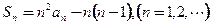
(Ⅰ)写出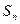 与
与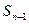 的递推关系式(
的递推关系式(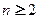 );
);
(Ⅱ)求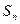 关于
关于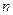 的表达式;
的表达式;
(Ⅲ)设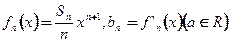 ,求数列
,求数列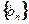 的前
的前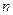 项和
项和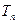 。
。
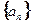 的前
的前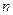 项和为
项和为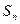 ,
,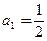 ,且
,且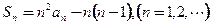
(Ⅰ)写出
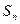 与
与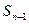 的递推关系式(
的递推关系式(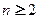 );
);(Ⅱ)求
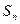 关于
关于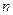 的表达式;
的表达式;(Ⅲ)设
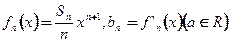 ,求数列
,求数列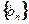 的前
的前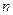 项和
项和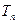 。
。(Ⅰ)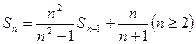 (Ⅱ)
(Ⅱ)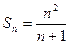 (Ⅲ)
(Ⅲ)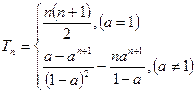
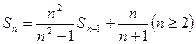 (Ⅱ)
(Ⅱ)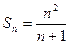 (Ⅲ)
(Ⅲ)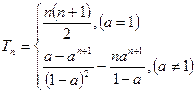
法1:(Ⅰ)由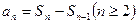 及
及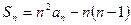 得
得
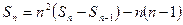 即
即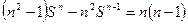
∴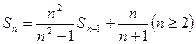
(Ⅱ)由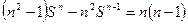 得
得
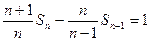
∴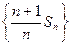 是首项为1,公差为1的等差数列,
是首项为1,公差为1的等差数列,
故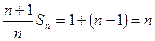
∴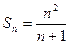
(Ⅲ)∵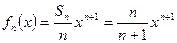
∴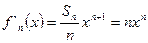
∴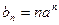
∴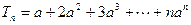 ………………①
………………①
当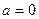 时,
时,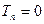 ;
;
当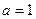 时,
时,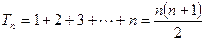 ;
;
当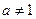 时
时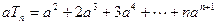 ………………②
………………②
由①-②得
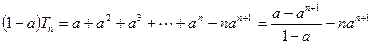 ;
;
∴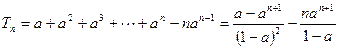
综上得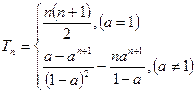 。
。
解法二、
(Ⅰ)由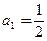 及
及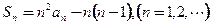 得
得
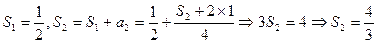
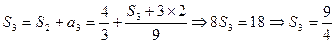
猜测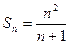 。用数学归纳法证明如下:
。用数学归纳法证明如下:
(1)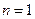 时,
时,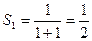 猜测成立;
猜测成立;
(2)假设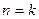 时,命题成立,即
时,命题成立,即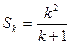 ,则
,则
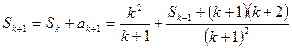
∴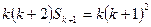 ,即
,即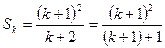 ,即
,即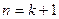 时命题也成立。
时命题也成立。
综合(1)、(2)知对于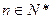 都有
都有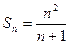
所以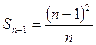 ,故
,故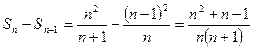 。
。
(Ⅱ)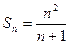 ,证明见(Ⅰ)。
,证明见(Ⅰ)。
(Ⅲ)同法一。
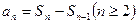 及
及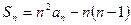 得
得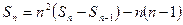 即
即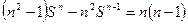
∴
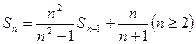
(Ⅱ)由
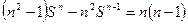 得
得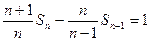
∴
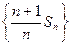 是首项为1,公差为1的等差数列,
是首项为1,公差为1的等差数列,故
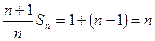
∴
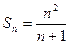
(Ⅲ)∵
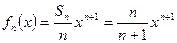
∴
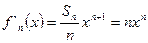
∴
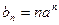
∴
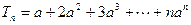 ………………①
………………①当
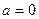 时,
时,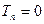 ;
;当
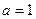 时,
时,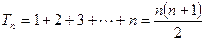 ;
;当
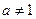 时
时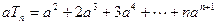 ………………②
………………②由①-②得
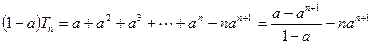 ;
;∴
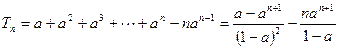
综上得
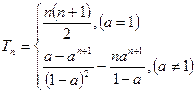 。
。解法二、
(Ⅰ)由
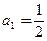 及
及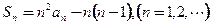 得
得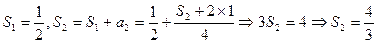
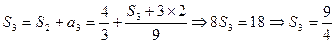
猜测
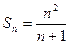 。用数学归纳法证明如下:
。用数学归纳法证明如下:(1)
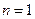 时,
时,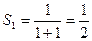 猜测成立;
猜测成立;(2)假设
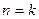 时,命题成立,即
时,命题成立,即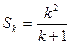 ,则
,则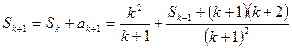
∴
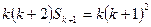 ,即
,即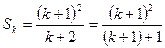 ,即
,即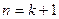 时命题也成立。
时命题也成立。综合(1)、(2)知对于
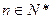 都有
都有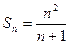
所以
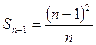 ,故
,故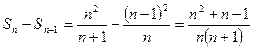 。
。(Ⅱ)
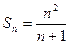 ,证明见(Ⅰ)。
,证明见(Ⅰ)。(Ⅲ)同法一。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
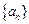 满足
满足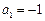 ,
,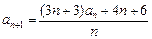 .(1)求
.(1)求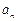 ;(2)令
;(2)令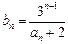 ,数列
,数列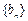 前
前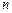 项和为
项和为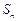 ,求证:当
,求证:当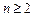 时,
时,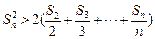 ;(3)证明:
;(3)证明: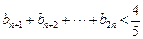 .
.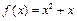 及正整数数列
及正整数数列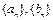 . 若
. 若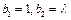 ,且当
,且当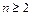 时,有
时,有 ; 又
; 又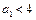 ,
,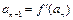 ,且
,且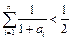 对任意
对任意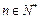 恒成立. 数列
恒成立. 数列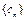 满足:
满足: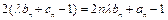 .
. 及
及 的通项公式;
的通项公式;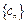 的前
的前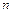 项和
项和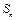 ;
;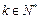 ,使得
,使得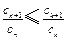 对任意
对任意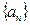 中,
中,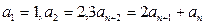 ,求数列
,求数列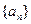 的首项为a,公差为b;等比数列
的首项为a,公差为b;等比数列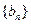 的首项为b,公比为a,其中a,
的首项为b,公比为a,其中a,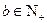 ,且
,且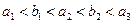 .
.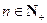 ,总存在
,总存在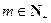 ,使
,使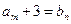 ,求b的值;
,求b的值;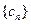 是所有
是所有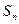 为
为
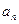 }的前n项和为
}的前n项和为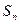 ,若
,若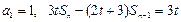 (t为正常数,n=2,3,4…).
(t为正常数,n=2,3,4…).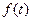 ,作数列
,作数列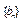 使
使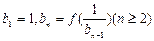 ,试求
,试求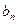 ,并求
,并求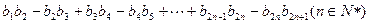
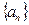 中,
中,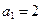 ,n≥2时
,n≥2时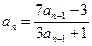 ,求通项公式.
,求通项公式.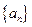 的前
的前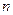 项和为
项和为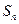 ,且
,且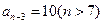 ,
,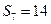 ,
,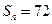 ,则
,则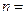 .
.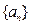 中,
中,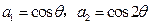 ,且
,且 .求
.求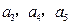 ,由此推出
,由此推出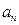 表达式.
表达式.