题目内容
(本题满分12分)已知数列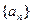 的前
的前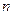 项和为
项和为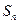 ,且满足
,且满足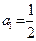 ,
,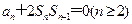 .(1)问:数列
.(1)问:数列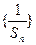 是否为等差数列?并证明你的结论;(2)求
是否为等差数列?并证明你的结论;(2)求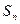 和
和 ;(3)求证:
;(3)求证: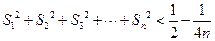 .
.
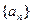 的前
的前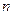 项和为
项和为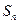 ,且满足
,且满足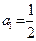 ,
,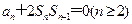 .(1)问:数列
.(1)问:数列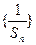 是否为等差数列?并证明你的结论;(2)求
是否为等差数列?并证明你的结论;(2)求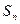 和
和 ;(3)求证:
;(3)求证: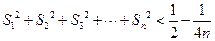 .
.(Ⅰ) 略 (Ⅱ) 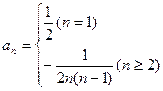 (Ⅲ)略
(Ⅲ)略
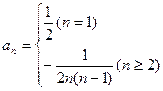 (Ⅲ)略
(Ⅲ)略(1)由已知有 ,
, ;
;  时,
时,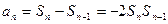
所以 ,即
,即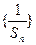 是以2为首项,公差为2 的等差数列. ….4分
是以2为首项,公差为2 的等差数列. ….4分
(2)由(1)得: ,
, ….6分
….6分
当 时,
时,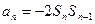
 .当
.当 时,
时,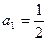 ,
,
所以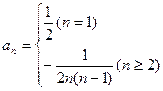 ….8分
….8分
(3)当 时,
时,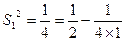 ,成立. 9分
,成立. 9分
当 时,
时,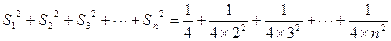 .10分
.10分
=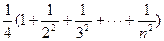


综上有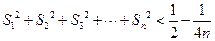 ….12分
….12分
 ,
, ;
;  时,
时,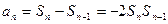
所以
 ,即
,即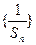 是以2为首项,公差为2 的等差数列. ….4分
是以2为首项,公差为2 的等差数列. ….4分(2)由(1)得:
 ,
, ….6分
….6分当
 时,
时,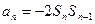
 .当
.当 时,
时,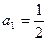 ,
,所以
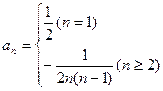 ….8分
….8分(3)当
 时,
时,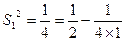 ,成立. 9分
,成立. 9分当
 时,
时,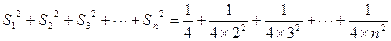 .10分
.10分=
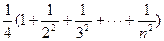


综上有
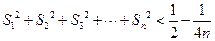 ….12分
….12分
练习册系列答案
相关题目
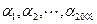 为2008个整数,且
为2008个整数,且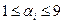 (
(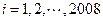 )。如果存在某个
)。如果存在某个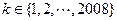 ,使得2008位数
,使得2008位数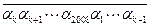 被101整除,试证明:对一切
被101整除,试证明:对一切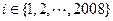 ,2008位数
,2008位数 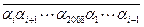 均能被101整除。
均能被101整除。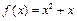 及正整数数列
及正整数数列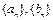 . 若
. 若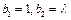 ,且当
,且当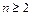 时,有
时,有 ; 又
; 又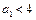 ,
,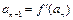 ,且
,且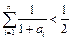 对任意
对任意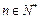 恒成立. 数列
恒成立. 数列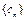 满足:
满足: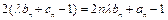 .
. 及
及 的通项公式;
的通项公式;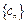 的前
的前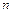 项和
项和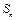 ;
;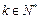 ,使得
,使得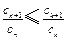 对任意
对任意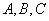 的机动车辆数如图所示(20,30;35,30;55,50),图中
的机动车辆数如图所示(20,30;35,30;55,50),图中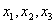 分别表示该时段单位时间通过路段
分别表示该时段单位时间通过路段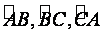 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则( )
的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则( )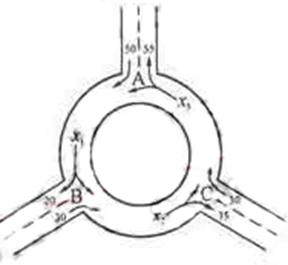
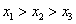
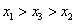
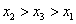
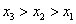
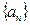 中,
中,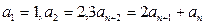 ,求数列
,求数列 是等差数列,若
是等差数列,若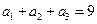 ,
,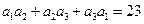 ,则
,则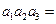 ( ).
( ).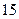
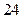
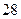
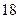
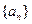 和数列
和数列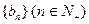 由下列条件确定:
由下列条件确定: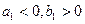 ;
;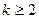 时,
时,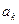 与
与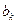 满足如下条件:当
满足如下条件:当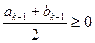 时,
时,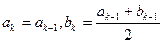 ;当
;当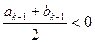 时,
时,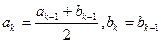 。
。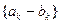 是等比数列;
是等比数列;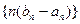 的前n项和为
的前n项和为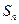 ;
;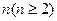 是满足
是满足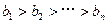 的最大整数时,用
的最大整数时,用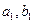 表示n的满足的条件。
表示n的满足的条件。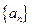 的通项公式是
的通项公式是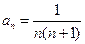 ,求其前
,求其前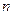 项和
项和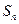 .
.