题目内容
10.已知α∈(-$\frac{π}{2}$,0),sinα=-$\frac{4}{5}$,则tan(α+$\frac{π}{4}$)=-$\frac{1}{7}$.分析 由同角三角函数基本关系可得tanα的值,再由两角和的正切公式可得.
解答 解:∵α∈(-$\frac{π}{2}$,0),sinα=-$\frac{4}{5}$,
∴cosα=$\sqrt{1-si{n}^{2}α}$=$\frac{3}{5}$,
∴tanα=$\frac{sinα}{cosα}$=-$\frac{4}{3}$,
∴tan(α+$\frac{π}{4}$)=$\frac{tanα+1}{1-tanα}$=-$\frac{1}{7}$
故答案为:-$\frac{1}{7}$.
点评 本题考查两角和与差的正切函数,涉及同角三角函数的基本关系,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.设A(1,-2),B(a,-1),C(-b,0),a>0,b>0,若A、B、C三点共线,则ab的最大值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |
18.不等式$\frac{x-2}{x+1}$<0的解集相同的是( )
| A. | $\left\{\begin{array}{l}{x-2>0}\\{x+1<0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-2<0}\\{x+1>0}\end{array}\right.$ | C. | (x-2)(x+1)<0 | D. | (x-2)(x+1)>0 |
15.不等式(x-y)(x+y)≥0所表示的平面区域为( )
| A. | 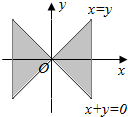 | B. | 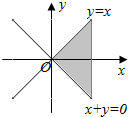 | C. | 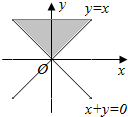 | D. | 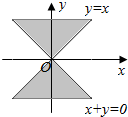 |