题目内容
设等差数列{an}的前n项和为Sn,且a3=6,S10=110.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}前n项和为Tn,且Tn=1-(
)an,令cn=anbn(n∈N*).求数列{cn}的前n项和Rn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}前n项和为Tn,且Tn=1-(
| ||
| 2 |
(Ⅰ)设等差数列{an}的公差为d,
∵a3=6,S10=110.
∴a1+2d=6,10a1+
d=110,
解得a1=2,d=2,
∴数列{an}的通项公式an=2+(n-1)•2=2n;
(Ⅱ)∵Tn=1-(
)an=1-(
)2n=1-(
)n,
当n=1时,b1=T1=1-(
)2=
,
当n≥2时,bn=Tn-Tn-1=1-(
)n-[1-(
)n-1]=(
)n,
且n=1时满足,
∴数列{an}的通项公式为bn=(
)n.
又an=2n,
∴cn=
=
,
∴Rn=
+
+
+…+
,
即
Rn=
+
+
+…+
,
两式相减得:
Rn=
+
+
+…+
-
=
-
=2-
,
∴Rn=4-
.
∵a3=6,S10=110.
∴a1+2d=6,10a1+
| 10×9 |
| 2 |
解得a1=2,d=2,
∴数列{an}的通项公式an=2+(n-1)•2=2n;
(Ⅱ)∵Tn=1-(
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
当n=1时,b1=T1=1-(
| ||
| 2 |
| 1 |
| 2 |
当n≥2时,bn=Tn-Tn-1=1-(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
且n=1时满足,
∴数列{an}的通项公式为bn=(
| 1 |
| 2 |
又an=2n,
∴cn=
| 2n |
| 2n |
| n |
| 2n-1 |
∴Rn=
| 1 |
| 20 |
| 2 |
| 21 |
| 3 |
| 22 |
| n |
| 2n-1 |
即
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
两式相减得:
| 1 |
| 2 |
| 1 |
| 20 |
| 1 |
| 21 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| n |
| 2n |
1-
| ||
1-
|
| n |
| 2n |
| n+2 |
| 2n |
∴Rn=4-
| n+2 |
| 2n-1 |

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
 的各项都是正数,且对任意
的各项都是正数,且对任意 都有
都有
 ,其中
,其中 为数列
为数列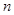 项和.
项和. 、
、 ;
; ,对任意的
,对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.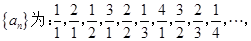 依它的前10项的规律,则
依它的前10项的规律,则 _.
_.