题目内容
已知数列{an}满足Sn=n2an(n∈N*),其中Sn是{an}的前n项和,且a1=1,求
(1)求an的表达式;
(2)求Sn.
(1)求an的表达式;
(2)求Sn.
(1)由Sn=n2an(n∈N*),得Sn-1=(n-1)2an-1(n≥2),
两式相减,得an=n2an-(n-1)2an-1,整理得
=
(n≥2),
∴n≥2时,an=a1×
×
×…×
=1×
×
×
×…×
=
,
又a1=1适合上式,
∴an=
;
(2)由(1)知,an=
=2(
-
),
∴Sn=2(1-
+
-
+…+
-
)=2(1-
)=
.
两式相减,得an=n2an-(n-1)2an-1,整理得
| an |
| an-1 |
| n-1 |
| n+1 |
∴n≥2时,an=a1×
| a2 |
| a1 |
| a3 |
| a2 |
| an |
| an-1 |
| 1 |
| 3 |
| 2 |
| 4 |
| 3 |
| 5 |
| n-1 |
| n+1 |
| 2 |
| n(n+1) |
又a1=1适合上式,
∴an=
| 2 |
| n(n+1) |
(2)由(1)知,an=
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Sn=2(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 2n |
| n+1 |

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 , 请从中归纳出第
, 请从中归纳出第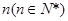 个等式:
个等式: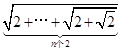 = ;
= ;