题目内容
已知数列 的各项都是正数,且对任意
的各项都是正数,且对任意 都有
都有
 ,其中
,其中 为数列
为数列 的前
的前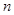 项和.
项和.
(1)求 、
、 ;
;
(2)求数列 的通项公式;
的通项公式;
(3)设 ,对任意的
,对任意的 ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 的各项都是正数,且对任意
的各项都是正数,且对任意 都有
都有
 ,其中
,其中 为数列
为数列 的前
的前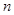 项和.
项和.(1)求
 、
、 ;
;(2)求数列
 的通项公式;
的通项公式;(3)设
 ,对任意的
,对任意的 ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.(1)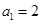 ,
,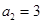 ;(2)
;(2)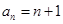 ;(3)
;(3)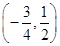 .
.
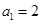 ,
,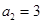 ;(2)
;(2)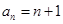 ;(3)
;(3)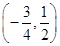 .
.试题分析:(1)分别令
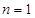 和
和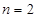 代入题干中的等式求出
代入题干中的等式求出 和
和 的值;(2)利用定义法进行求解,在原式中利用
的值;(2)利用定义法进行求解,在原式中利用 替换
替换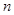 得到
得到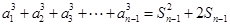 ,将此等式与原式作差得到
,将此等式与原式作差得到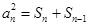
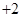 ,再次利用定义法得到数列
,再次利用定义法得到数列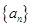 为等差数列,最后利用等差数列的通项公式进行求解;(3)利用
为等差数列,最后利用等差数列的通项公式进行求解;(3)利用 化简得到
化简得到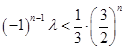 ,对
,对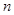 进行分奇偶讨论求出
进行分奇偶讨论求出 的取值范围.
的取值范围.试题解析:(1)令
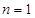 ,则
,则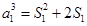 ,即
,即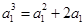 ,所以
,所以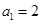 或
或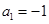 或
或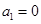 ,
,又因为数列
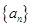 的各项都是正数,所以
的各项都是正数,所以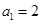 ,
,令
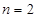 ,则
,则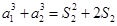 ,即
,即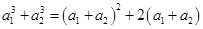 ,解得
,解得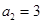 或
或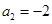 或
或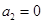 ,
,又因为数列
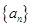 的各项都是正数,所以
的各项都是正数,所以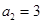 ,
,(2)
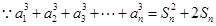 , ①
, ①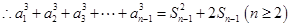 , ②
, ②由①
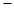 ②得
②得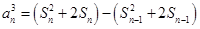 ,
,化简得到
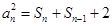 , ③
, ③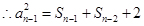 ,④
,④由③
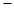 ④得
④得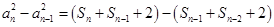 ,
,化简得到
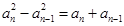 ,即
,即 ,
,当
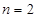 时,
时,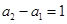 ,所以
,所以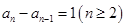 ,
,所以数列
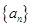 是一个以
是一个以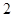 为首项,
为首项, 为公差的等差数列,
为公差的等差数列,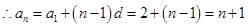 ;
;(3)
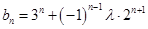 ,
,因为对任意的
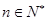 ,都有
,都有 恒成立,即有
恒成立,即有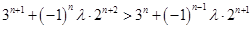 ,
,化简得
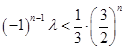 ,
,当
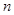 为奇数时,
为奇数时, 恒成立,
恒成立,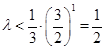 ,即
,即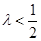 ,
,当
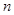 为偶数时,
为偶数时,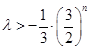 恒成立,
恒成立, ,即
,即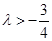 ,
, ,故实数
,故实数 的取值范围是
的取值范围是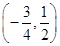 .
.
练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
 (
(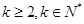 )的数列
)的数列 、
、 、
、 前
前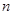 项的和分别为
项的和分别为 、
、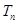 、
、 .已知集合
.已知集合 =
= .
. ,求数列
,求数列
 ,试研究
,试研究 和
和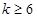 时是否存在符合条件的数列对(
时是否存在符合条件的数列对( ,对于固定的
,对于固定的 , 请从中归纳出第
, 请从中归纳出第 个等式:
个等式: = ;
= ;
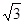 ,3,
,3,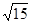 ,
,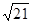 ,
,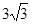 ,…,则9是这个数列的第( )
,…,则9是这个数列的第( ) 满足
满足 ,则
,则 .
. 满足
满足 ,
, ,则
,则 ( )
( )