题目内容
已知等差数列{an}中,首项a1=1,公差d为整数,且满足a1+3<a3,a2+5>a4,数列{bn}满足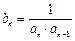 ,其前n项和为Sn.(1)求数列{an}的通项公式an;(2)若S2为S1,Sm(m∈N*)的等比中项,求m的值.
,其前n项和为Sn.(1)求数列{an}的通项公式an;(2)若S2为S1,Sm(m∈N*)的等比中项,求m的值.
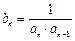 ,其前n项和为Sn.(1)求数列{an}的通项公式an;(2)若S2为S1,Sm(m∈N*)的等比中项,求m的值.
,其前n项和为Sn.(1)求数列{an}的通项公式an;(2)若S2为S1,Sm(m∈N*)的等比中项,求m的值.(Ⅰ) an=2n-1 (Ⅱ) m=12
解:(1)由题意,得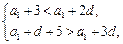 解得
解得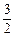 < d <
< d <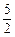 .……3分
.……3分
又d∈Z,∴d = 2.∴an=1+(n-1)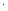 2=2n-1.……6分
2=2n-1.……6分
(2)∵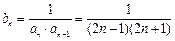
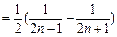 ,
,
∴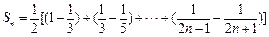
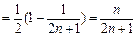 .11分
.11分
∵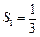 ,
,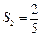 ,
,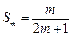 ,S2为S1,Sm(m∈
,S2为S1,Sm(m∈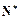 )的等比中项,
)的等比中项,
∴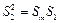 ,即
,即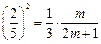 , …14分解得m=12.…15分
, …14分解得m=12.…15分
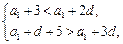 解得
解得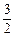 < d <
< d <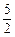 .……3分
.……3分又d∈Z,∴d = 2.∴an=1+(n-1)
 2=2n-1.……6分
2=2n-1.……6分(2)∵
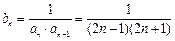
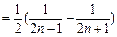 ,
,∴
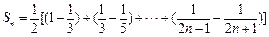
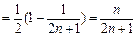 .11分
.11分∵
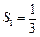 ,
,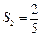 ,
,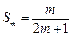 ,S2为S1,Sm(m∈
,S2为S1,Sm(m∈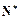 )的等比中项,
)的等比中项,∴
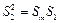 ,即
,即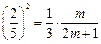 , …14分解得m=12.…15分
, …14分解得m=12.…15分
练习册系列答案
相关题目
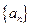 满足
满足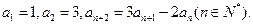
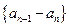 是等比数列; (II)求数列
是等比数列; (II)求数列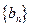 满足
满足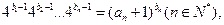 证明
证明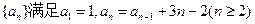
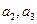 ; (II)求数列
; (II)求数列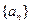 的通项公式。
的通项公式。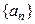 满足
满足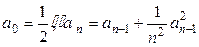 其中n=1,2,3,….
其中n=1,2,3,….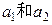 的值;
的值;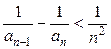 ;
;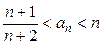 .
.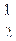 (3n+Sn)对一切正整数n成立
(3n+Sn)对一切正整数n成立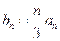 ,求数列
,求数列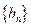 的前n项和Bn;
的前n项和Bn;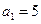 ,且
,且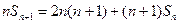 ( n∈N*),则过点P(n,
( n∈N*),则过点P(n,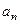 ) 和Q(n+2,
) 和Q(n+2,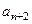 )( n∈N*)的直线的一个方向向量的坐标可以是 ( )
)( n∈N*)的直线的一个方向向量的坐标可以是 ( ) )
) , -1)?
, -1)? )
)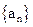 满足
满足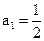 ,且
,且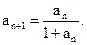
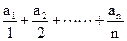
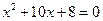
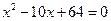
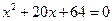
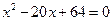
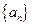 的前
的前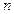 项和为
项和为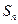 ,若
,若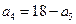 ,则
,则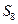 等于 ()
等于 ()