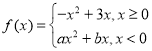题目内容
【题目】已知动点![]() 到定直线
到定直线![]() 的距离比到定点
的距离比到定点![]() 的距离大
的距离大![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线交轨迹
的直线交轨迹![]() 于
于![]() ,
, ![]() 两点,直线
两点,直线![]() ,
, ![]() 分别交直线
分别交直线![]() 于点
于点![]() ,
, ![]() ,证明以
,证明以![]() 为直径的圆被
为直径的圆被![]() 轴截得的弦长为定值,并求出此定值.
轴截得的弦长为定值,并求出此定值.
【答案】(I)![]() ;(II)详见解析.
;(II)详见解析.
【解析】
试题分析:(1)依据题设条件及两点间距离公式建立方程分析求解;(2)依据题设条件建立直线![]() ,
,![]() 的方程,再运用坐标之间的关系分析探求:
的方程,再运用坐标之间的关系分析探求:
试题解析:
解:(Ⅰ)设点![]() 的坐标为
的坐标为![]() ,因为定点
,因为定点![]() 在定直线
在定直线![]() :
:![]() 的右侧,
的右侧,
且动点![]() 到定直线
到定直线![]() :
:![]() 的距离比到定点
的距离比到定点![]() 的距离大
的距离大![]() ,
,
所以![]() 且
且![]() ,
,
化简得![]() ,即
,即![]() ,
,
轨迹![]() 的方程为
的方程为![]() .
.

(Ⅱ)设![]() ,
,![]() (
(![]() ),则
),则![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,![]() 三点共线,
三点共线,
∴![]() ,
,
∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
直线![]() 的方程为
的方程为![]() ,令
,令![]() ,得
,得![]() .
.
同理可得![]() .
.
所以以![]() 为直径的圆的方程为
为直径的圆的方程为![]() ,
,
即![]() .
.
将![]() 代入上式,可得
代入上式,可得![]() ,
,
令![]() ,即
,即![]() 或
或![]() ,
,
故以![]() 为直径的圆被
为直径的圆被![]() 轴截得的弦长为定值4.
轴截得的弦长为定值4.

练习册系列答案
相关题目