题目内容
【题目】已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,其离心率
,其离心率![]() ,焦距为4.
,焦距为4.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 是椭圆上不重合的四个点,且满足
是椭圆上不重合的四个点,且满足![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(Ⅰ)由已知,![]() ,求出
,求出![]() ,
,![]() ,即可得到椭圆
,即可得到椭圆![]() 的方程;
的方程;
(Ⅱ)由满足∵![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,
,![]() ,可得直线
,可得直线![]() 垂直相交于点
垂直相交于点![]() .1,由(1)椭圆方程)
.1,由(1)椭圆方程)![]() ,F1(-2,0).
,F1(-2,0).
①直线AC,BD有一条斜率不存在时,|![]() .
.
②直线![]() 斜率均存在,则斜率均不为0,不妨设
斜率均存在,则斜率均不为0,不妨设![]() 方程
方程![]()
联立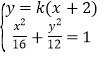 ,得
,得![]() .利用根与系数的关系可得:
.利用根与系数的关系可得:![]() ,把
,把![]() 代入上式可得:
代入上式可得:![]() ,可得|
,可得|![]() ,即可得出.
,即可得出.
(Ⅰ)由已知,![]() ,∴
,∴![]() ,∴
,∴![]()
故,椭圆方程为![]() 。
。
(Ⅱ)∵![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,
,![]() ,∴直线
,∴直线![]() 垂直相交于点
垂直相交于点![]() .
.
①直线![]() 有一条斜率不存在时,
有一条斜率不存在时,![]()
②直线![]() 斜率均存在,则斜率均不为0,不妨设
斜率均存在,则斜率均不为0,不妨设![]() 方程
方程![]()
联立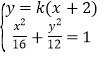 ,得
,得![]()
![]()
设![]() ,则
,则![]()
![]() .把
.把![]() 代入上式可得:
代入上式可得:![]() ,
,
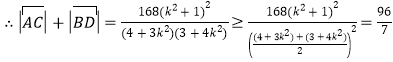 ,
,
当且仅当![]() ,即
,即![]() 时,上式取等号
时,上式取等号
综上可得:![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
【题目】某单位共有10名员工,他们某年的收入如下表:
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪(万元) | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
(1)求该单位员工当年年薪的平均值和中位数;
(2)已知员工年薪收入与工作年限成正相关关系,某员工工作第一年至第四年的年薪分别为4万元、5.5万元、6万元、8.5万元,预测该员工第六年的年薪为多少?
附:线性回归方程![]() 中系数计算公式分别为:
中系数计算公式分别为: ,
,![]() ,其中
,其中![]() 、
、![]() 为样本均值.
为样本均值.
