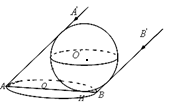
题目内容
(本小题满分14分)
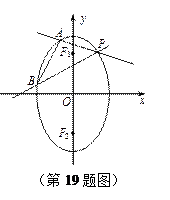
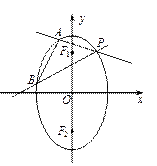
如图,椭圆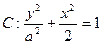
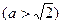 的离心率为
的离心率为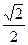 ,其两焦点分别为
,其两焦点分别为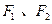 ,
,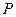 是椭圆在第一象限弧上一点,并满足
是椭圆在第一象限弧上一点,并满足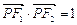 ,过
,过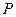 作倾斜角互补的两条直线
作倾斜角互补的两条直线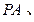
 分别交椭圆于
分别交椭圆于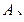
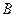 两点.
两点.
(1)求椭圆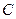
 的方程.
的方程.
(2)求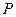 点坐标;
点坐标; 
(3)当直线 的斜率为
的斜率为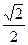 时,求直线
时,求直线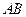 的方程.
的方程.
如图,椭圆
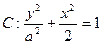
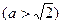 的离心率为
的离心率为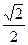 ,其两焦点分别为
,其两焦点分别为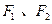 ,
,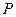 是椭圆在第一象限弧上一点,并满足
是椭圆在第一象限弧上一点,并满足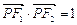 ,过
,过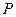 作倾斜角互补的两条直线
作倾斜角互补的两条直线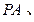
 分别交椭圆于
分别交椭圆于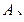
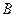 两点.
两点. (1)求椭圆
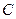
 的方程.
的方程.(2)求
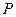 点坐标;
点坐标; 
(3)当直线
 的斜率为
的斜率为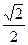 时,求直线
时,求直线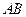 的方程.
的方程. 
(1)
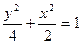
(2)
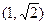
(3)
 方程为
方程为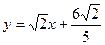
解:(1)由椭圆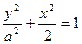
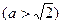 的离心率为
的离心率为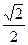 ,得
,得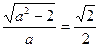 ,………2分
,………2分
解得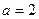 . …………3分
. …………3分
所以椭圆 的方程为:
的方程为: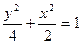 . …………4分
. …………4分
(2)由题意可得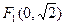 ,
,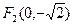 , …………5分
, …………5分
设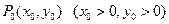 ,
,
则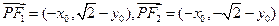 ,
,
所以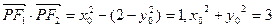 . …………6分
. …………6分
又因为点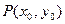 在曲线上,则
在曲线上,则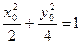 ,
,
所以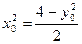 , …………7分
, …………7分
从而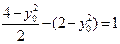 ,得
,得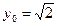 (因在第一象限), …………8分
(因在第一象限), …………8分
则点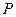 的坐标为
的坐标为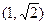 . …………9分
. …………9分
(3)由题意知 的斜率为
的斜率为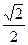 ,
,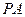 的斜率为
的斜率为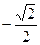 ,则
,则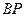 的直线方程为:
的直线方程为: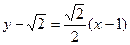 . …………10分
. …………10分
由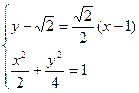 得
得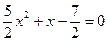 .……11分
.……11分
设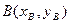 ,则
,则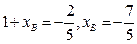 ,……12分
,……12分
同理可得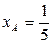 ,则
,则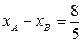 ,
,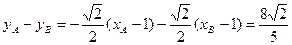 , …………13分
, …………13分
所以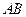 的斜率
的斜率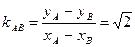 ,
, 方程为
方程为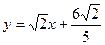 .………14分
.………14分
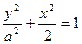
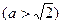 的离心率为
的离心率为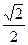 ,得
,得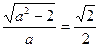 ,………2分
,………2分
解得
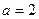 . …………3分
. …………3分所以椭圆
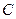 的方程为:
的方程为: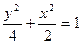 . …………4分
. …………4分(2)由题意可得
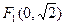 ,
,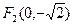 , …………5分
, …………5分设
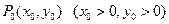 ,
,则
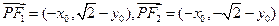 ,
,所以
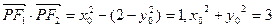 . …………6分
. …………6分又因为点
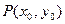 在曲线上,则
在曲线上,则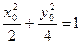 ,
,所以
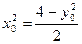 , …………7分
, …………7分从而
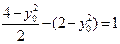 ,得
,得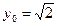 (因在第一象限), …………8分
(因在第一象限), …………8分则点
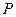 的坐标为
的坐标为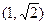 . …………9分
. …………9分(3)由题意知
 的斜率为
的斜率为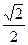 ,
,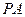 的斜率为
的斜率为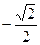 ,则
,则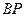 的直线方程为:
的直线方程为: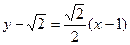 . …………10分
. …………10分 由
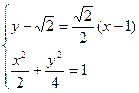 得
得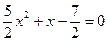 .……11分
.……11分设
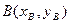 ,则
,则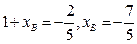 ,……12分
,……12分同理可得
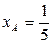 ,则
,则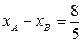 ,
,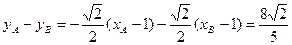 , …………13分
, …………13分所以
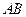 的斜率
的斜率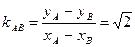 ,
,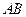 方程为
方程为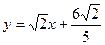 .………14分
.………14分
练习册系列答案
相关题目
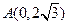 ,离心率为
,离心率为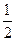
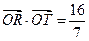 .若存在,求直线l的方程;若不存在,请说明理由.
.若存在,求直线l的方程;若不存在,请说明理由.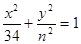 和双曲线
和双曲线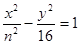 有相同的焦点,则实数
有相同的焦点,则实数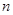 的值是( )
的值是( )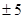 B
B 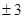 C 5 D 9
C 5 D 9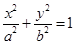 和
和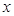 轴正方向交点为A,和
轴正方向交点为A,和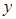 轴正方向的交点为B,P为第一象限内椭圆上的点,使四边形OAPB面积最大(O为原点),那么四边形OAPB面积最大值为( )
轴正方向的交点为B,P为第一象限内椭圆上的点,使四边形OAPB面积最大(O为原点),那么四边形OAPB面积最大值为( )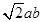
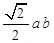
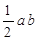
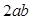
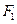 、
、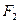 在x轴上,点P为椭圆上的一个动点,且
在x轴上,点P为椭圆上的一个动点,且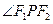 的最大值为90°,直线l过左焦点
的最大值为90°,直线l过左焦点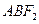 的面积最大值为12.
的面积最大值为12.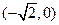 ,
,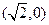 ,离心率是
,离心率是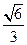 ,直线
,直线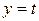 椭圆C交与不同的两点M,N,以线段MN为直径作圆P,圆心为P。
椭圆C交与不同的两点M,N,以线段MN为直径作圆P,圆心为P。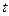 的值;
的值; 果椭圆
果椭圆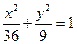 的弦被点(4,2)平分,则这条弦所在的直线方程是
的弦被点(4,2)平分,则这条弦所在的直线方程是 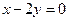
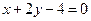
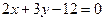
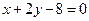
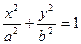 (
(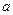
 ),篮球与地面的接触点为H,则|OH|= .
),篮球与地面的接触点为H,则|OH|= .