جâؤ؟ؤعبف
،¾جâؤ؟،؟ؤ³²âتشحإ¶سخھءثرذ¾؟،°زû¾ئ،±¶ش،°¼ف³µ°²ب«،±µؤس°دى£¬ثو»ْر،ب،![]() أû¼فت»ش±دب؛َشعخق¾ئ×´ج¬،¢¾ئ؛َ×´ج¬دآ½ّذذ،°ح£³µ¾àہë،±²âتش£¬²âتشµؤ·½°¸£؛µçؤشؤ£ؤâ¼فت»£¬زشؤ³ثظ¶بشبثظذذت»£¬¼اآ¼دآ¼فت»ش±µؤ،°ح£³µ¾àہë،±£¨¼فت»ش±´س؟´µ½زâحâاé؟ِµ½³µ×سح£دآثùذèزھµؤ¾àہ룩£¬خق¾ئ×´ج¬سë¾ئ؛َ×´ج¬دآµؤتشرéت¾ف·ض±ًءذسع±ي
أû¼فت»ش±دب؛َشعخق¾ئ×´ج¬،¢¾ئ؛َ×´ج¬دآ½ّذذ،°ح£³µ¾àہë،±²âتش£¬²âتشµؤ·½°¸£؛µçؤشؤ£ؤâ¼فت»£¬زشؤ³ثظ¶بشبثظذذت»£¬¼اآ¼دآ¼فت»ش±µؤ،°ح£³µ¾àہë،±£¨¼فت»ش±´س؟´µ½زâحâاé؟ِµ½³µ×سح£دآثùذèزھµؤ¾àہ룩£¬خق¾ئ×´ج¬سë¾ئ؛َ×´ج¬دآµؤتشرéت¾ف·ض±ًءذسع±ي![]()
ح£³µ¾àہë |
|
|
|
|
|
ئµت | 26 |
|
| 8 | 2 |
±ي![]()
ئ½¾ùأ؟؛ءةرھز؛¾ئ¾«؛¬ء؟ | 10 | 30 | 50 | 70 | 90 | /tr>
ئ½¾ùح£³µ¾àہë | 30 | 50 | 60 | 70 | 90 |
زرضھ±ي![]() ت¾فµؤضذخ»ت¹ہ¼ئضµخھ
ت¾فµؤضذخ»ت¹ہ¼ئضµخھ![]() £¬»ط´ًزشدآختجâ.
£¬»ط´ًزشدآختجâ.
(¢ٌ)اَ![]() µؤضµ£¬²¢¹ہ¼ئ¼فت»ش±خق¾ئ×´ج¬دآح£³µ¾àہëµؤئ½¾ùت£»
µؤضµ£¬²¢¹ہ¼ئ¼فت»ش±خق¾ئ×´ج¬دآح£³µ¾àہëµؤئ½¾ùت£»
£¨¢ٍ£©¸ù¾ف×îذ،¶³ث·¨£¬سة±ي![]() µؤت¾ف¼ئثم
µؤت¾ف¼ئثم![]() ¹طسع
¹طسع![]() µؤ»ط¹é·½³ج
µؤ»ط¹é·½³ج![]() £»
£»
£¨¢َ£©¸أ²âتشحإ¶سبدخھ£؛¼فت»ش±¾ئ؛َ¼ف³µµؤئ½¾ù،°ح£³µ¾àہë،±![]() ´َسع£¨¢ٌ£©ضذخق¾ئ×´ج¬دآµؤح£³µ¾àہëئ½¾ùتµؤ
´َسع£¨¢ٌ£©ضذخق¾ئ×´ج¬دآµؤح£³µ¾àہëئ½¾ùتµؤ![]() ±¶£¬شٍبد¶¨¼فت»ش±تا،°×ي¼ف،±.اë¸ù¾ف(¢ٍ)ضذµؤ»ط¹é·½³ج,ش¤²âµ±أ؟؛ءةرھز؛¾ئ¾«؛¬ء؟´َسع¶àةظ؛ء؟ثت±خھ،°×ي¼ف،±£؟
±¶£¬شٍبد¶¨¼فت»ش±تا،°×ي¼ف،±.اë¸ù¾ف(¢ٍ)ضذµؤ»ط¹é·½³ج,ش¤²âµ±أ؟؛ءةرھز؛¾ئ¾«؛¬ء؟´َسع¶àةظ؛ء؟ثت±خھ،°×ي¼ف،±£؟
£¨¸½£؛»ط¹é·½³ج![]() ضذ£¬
ضذ£¬ 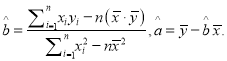 £©
£©
،¾´ً°¸،؟£¨¢ٌ£©![]() £»£¨¢ٍ£©
£»£¨¢ٍ£© ![]() £»£¨¢َ£©بد¶¨خھ،°×ي¼ف،±.
£»£¨¢َ£©بد¶¨خھ،°×ي¼ف،±.
،¾½âخِ،؟تشجâ·ضخِ£؛(¢ٌ£©¸ù¾ف±ي1¼°ضذخ»تµؤ¸إؤî؟ةاَ³ِ![]() £»£¨¢ٍ£©سة»ط¹éدµت¹«ت½اَ³ِ
£»£¨¢ٍ£©سة»ط¹éدµت¹«ت½اَ³ِ![]() ¼´؟ة£»£¨¢َ£©سة£¨¢ٌ£©ضھµ±
¼´؟ة£»£¨¢َ£©سة£¨¢ٌ£©ضھµ±![]() ت±بد¶¨¼فت»ش±تا،°×ي¼ف،±£¬ءî
ت±بد¶¨¼فت»ش±تا،°×ي¼ف،±£¬ءî![]() £¬µأ
£¬µأ![]() £¬½âµأ
£¬½âµأ![]() £¬µ±أ؟؛ءةرھز؛¾ئ¾«؛¬ء؟´َسع
£¬µ±أ؟؛ءةرھز؛¾ئ¾«؛¬ء؟´َسع![]() ؛ء؟ثت±بد¶¨خھ،°×ي¼ف،±£®
؛ء؟ثت±بد¶¨خھ،°×ي¼ف،±£®
تشجâ½âخِ£؛£¨¢ٌ£©زہجâز⣬µأ![]() £¬½âµأ
£¬½âµأ![]() £¬
£¬
سض![]() £¬½âµأ
£¬½âµأ![]() £»
£»
¹تح£³µ¾àہëµؤئ½¾ùتخھ![]()
£¨¢ٍ£©زہجâز⣬؟ةضھ![]() £¬
£¬
![]()
![]() ,
,
![]() ,
,
ثùزش»ط¹éض±دكخھ![]()
£¨¢َ£©سة£¨¢ٌ£©ضھµ±![]() ت±بد¶¨¼فت»ش±تا،°×ي¼ف،±
ت±بد¶¨¼فت»ش±تا،°×ي¼ف،±
ءî![]() £¬µأ
£¬µأ![]() £¬½âµأ
£¬½âµأ![]() ,
,
µ±أ؟؛ءةرھز؛¾ئ¾«؛¬ء؟´َسع![]() ؛ء؟ثت±بد¶¨خھ،°×ي¼ف،±£®
؛ء؟ثت±بد¶¨خھ،°×ي¼ف،±£®

 ؟ھذؤتش¾يئعؤ©³ه´ج100·ضدµءذ´ً°¸
؟ھذؤتش¾يئعؤ©³ه´ج100·ضدµءذ´ً°¸ ث«»ùح¬²½µ¼؛½رµء·دµءذ´ً°¸
ث«»ùح¬²½µ¼؛½رµء·دµءذ´ً°¸