题目内容
【题目】在斜三棱柱![]() 中,
中,![]() ,平面
,平面![]() 底面
底面![]() ,点
,点![]() 、D分别是线段
、D分别是线段![]() 、BC的中点.
、BC的中点.

(1)求证:![]() ;
;
(2)求证:AD//平面![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:
(1)利用题意证得AD⊥平面![]() ,结合线面垂直的定义可得AD⊥CC1.
,结合线面垂直的定义可得AD⊥CC1.
(2)利用题意可得EM // AD,结合题意和线面平行的判断法则即可证得结论.
试题解析:
证明:(1)∵AB![]() AC,点D是线段BC的中点,∴AD⊥BC.
AC,点D是线段BC的中点,∴AD⊥BC.
又∵平面![]() 底面
底面![]() ,AD
,AD![]() 平面ABC,平面
平面ABC,平面![]() 底面
底面![]() ,
,
∴AD⊥平面![]() .
.
又CC1![]() 平面
平面![]() ,∴AD⊥CC1.
,∴AD⊥CC1.
(2)连结B1C与BC1交于点E,连结EM,DE.
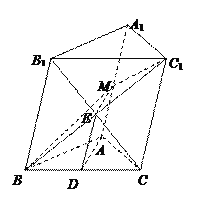
在斜三棱柱![]() 中,四边形BCC1B1是平行四边∴点E为B1C的中点.
中,四边形BCC1B1是平行四边∴点E为B1C的中点.
∵点D是BC的中点,∴DE//B1B,DE![]() B1B. ……10分
B1B. ……10分
又∵点M是平行四边形BCC1B1边AA1的中点,
∴AM//B1B,AM![]() B1B.∴AM// DE,AM
B1B.∴AM// DE,AM![]() DE.
DE.
∴四边形ADEM是平行四边形.
∴EM // AD.
又EM![]() 平面MBC1,AD
平面MBC1,AD![]() 平面MBC1,
平面MBC1,
∴AD //平面MBC1.

 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案【题目】某研究所设计了一款智能机器人,为了检验设计方案中机器人动作完成情况,现委托某工厂生产![]() 个机器人模型,并对生产的机器人进行编号:
个机器人模型,并对生产的机器人进行编号: ![]() ,采用系统抽样的方法抽取一个容量为
,采用系统抽样的方法抽取一个容量为![]() 的机器人样本,试验小组对
的机器人样本,试验小组对![]() 个机器人样本的动作个数进行分组,频率分布直方图及频率分布表中的部分数据如图所示,请据此回答如下问题:
个机器人样本的动作个数进行分组,频率分布直方图及频率分布表中的部分数据如图所示,请据此回答如下问题:
分组 | 机器人数 | 频率 |
| 0.08 | |
| 10 | |
| 10 | |
| ||
| 6 |

(1)补全频率分布表,画出频率分布直方图;
(2)若随机抽的第一个号码为![]() ,这
,这![]() 个机器人分别放在
个机器人分别放在![]() 三个房间,从
三个房间,从![]() 到
到![]() 在
在![]() 房间,从
房间,从![]() 到
到![]() 在
在![]() 房间,从
房间,从![]() 到
到![]() 在
在![]() 房间,求
房间,求![]() 房间被抽中的人数是多少?
房间被抽中的人数是多少?
(3)从动作个数不低于![]() 的机器人中随机选取
的机器人中随机选取![]() 个机器人,该
个机器人,该![]() 个机器人中动作个数不低于
个机器人中动作个数不低于![]() 的机器人记为
的机器人记为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
【题目】某测试团队为了研究“饮酒”对“驾车安全”的影响,随机选取![]() 名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试,测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子停下所需要的距离),无酒状态与酒后状态下的试验数据分别列于表
名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试,测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子停下所需要的距离),无酒状态与酒后状态下的试验数据分别列于表![]()
停车距离 |
|
|
|
|
|
频数 | 26 |
|
| 8 | 2 |
表![]()
平均每毫升血液酒精含量 | 10 | 30 | 50 | 70 | 90 | /tr>
平均停车距离 | 30 | 50 | 60 | 70 | 90 |
已知表![]() 数据的中位数估计值为
数据的中位数估计值为![]() ,回答以下问题.
,回答以下问题.
(Ⅰ)求![]() 的值,并估计驾驶员无酒状态下停车距离的平均数;
的值,并估计驾驶员无酒状态下停车距离的平均数;
(Ⅱ)根据最小二乘法,由表![]() 的数据计算
的数据计算![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(Ⅲ)该测试团队认为:驾驶员酒后驾车的平均“停车距离”![]() 大于(Ⅰ)中无酒状态下的停车距离平均数的
大于(Ⅰ)中无酒状态下的停车距离平均数的![]() 倍,则认定驾驶员是“醉驾”.请根据(Ⅱ)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
倍,则认定驾驶员是“醉驾”.请根据(Ⅱ)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
(附:回归方程![]() 中,
中, 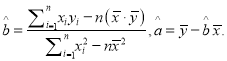 )
)
