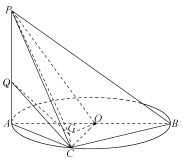
题目内容
【题目】已知函数![]() ,
, ![]() (
(![]() ,
, ![]() 为自然对数的底数).
为自然对数的底数).
(1)试讨论函数![]() 的极值情况;
的极值情况;
(2)证明:当![]() 且
且![]() 时,总有
时,总有![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)求![]() 定义域内的所有根;判断
定义域内的所有根;判断![]() 的根
的根![]() 左右两侧值的符号即可得结果;(2)当
左右两侧值的符号即可得结果;(2)当![]() 时,
时, ![]()
![]() ,研究函数的单调性,两次求导,可证明
,研究函数的单调性,两次求导,可证明![]() 在
在![]() 内为单调递增函数,进而可得当
内为单调递增函数,进而可得当![]() 时,
时, ![]() ,即可得结果.
,即可得结果.
试题解析:(1)![]() 的定义域为
的定义域为![]() ,
,
![]()
![]() .
.
①当![]() 时,
时, ![]() ,故
,故![]() 在
在![]() 内单调递减,
内单调递减, ![]() 无极值;
无极值;
②当![]() 时,令
时,令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() .
.
故![]() 在
在![]() 处取得极大值,且极大值为
处取得极大值,且极大值为![]() ,
, ![]() 无极小值.
无极小值.
(2)证法一:当![]() 时,
时, ![]()
![]()
![]() .
.
设函数![]()
![]() ,
,
则![]() .记
.记![]() ,
,
则![]() .
.
当![]() 变化时,
变化时, ![]() ,
, ![]() 的变化情况如下表:
的变化情况如下表:

由上表可知![]() ,
,
而![]()
![]()
![]() ,
,
由![]() ,知
,知![]() ,
,
所以![]() ,
,
所以![]() ,即
,即![]() .
.
所以![]() 在
在![]() 内为单调递增函数.
内为单调递增函数.
所以当![]() 时,
时, ![]() .
.
即当![]() 且
且![]() 时,
时, ![]()
![]() .
.
所以当![]() 且
且![]() 时,总有
时,总有![]() .
.
证法二:当![]() 时,
时, ![]()
![]()
![]() .
.
因为![]() 且
且![]() ,故只需证
,故只需证![]() .
.
当![]() 时,
时, ![]() 成立;
成立;
当![]() 时,
时, ![]() ,即证
,即证![]() .
.
令![]() ,则由
,则由![]() ,得
,得![]() .
.
在![]() 内,
内, ![]() ;
;
在![]() 内,
内, ![]() ,
,
所以![]() .
.
故当![]() 时,
时, ![]() 成立.
成立.
综上得原不等式成立.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案【题目】某测试团队为了研究“饮酒”对“驾车安全”的影响,随机选取![]() 名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试,测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子停下所需要的距离),无酒状态与酒后状态下的试验数据分别列于表
名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试,测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子停下所需要的距离),无酒状态与酒后状态下的试验数据分别列于表![]()
停车距离 |
|
|
|
|
|
频数 | 26 |
|
| 8 | 2 |
表![]()
平均每毫升血液酒精含量 | 10 | 30 | 50 | 70 | 90 | /tr>
平均停车距离 | 30 | 50 | 60 | 70 | 90 |
已知表![]() 数据的中位数估计值为
数据的中位数估计值为![]() ,回答以下问题.
,回答以下问题.
(Ⅰ)求![]() 的值,并估计驾驶员无酒状态下停车距离的平均数;
的值,并估计驾驶员无酒状态下停车距离的平均数;
(Ⅱ)根据最小二乘法,由表![]() 的数据计算
的数据计算![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(Ⅲ)该测试团队认为:驾驶员酒后驾车的平均“停车距离”![]() 大于(Ⅰ)中无酒状态下的停车距离平均数的
大于(Ⅰ)中无酒状态下的停车距离平均数的![]() 倍,则认定驾驶员是“醉驾”.请根据(Ⅱ)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
倍,则认定驾驶员是“醉驾”.请根据(Ⅱ)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
(附:回归方程![]() 中,
中, 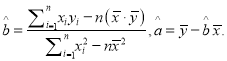 )
)