题目内容
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
设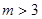 ,对于项数为
,对于项数为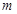 的有穷数列
的有穷数列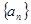 ,令
,令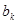 为
为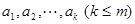 中最大值,称数列
中最大值,称数列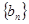 为
为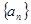 的“创新数列”.例如数列
的“创新数列”.例如数列 3,5,4,7的创新数列为3,5,5,7.
3,5,4,7的创新数列为3,5,5,7.
考查自然数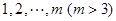 的所有排列,将每种排列都视为一个有穷数列
的所有排列,将每种排列都视为一个有穷数列 .
.
(1)若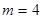 ,写出创新数列为3,4,4,4的所有数列
,写出创新数列为3,4,4,4的所有数列 ;
;
(2)是否存在数列 的创新数列为等比数列?若存在,求出符合条件的创新数列;若不存在,请说明理由.
的创新数列为等比数列?若存在,求出符合条件的创新数列;若不存在,请说明理由.
(3)是否存在数列 ,使它的创新数列为等差数列?若存在,求出满足所有条件的数列
,使它的创新数列为等差数列?若存在,求出满足所有条件的数列 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.
设
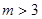 ,对于项数为
,对于项数为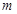 的有穷数列
的有穷数列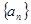 ,令
,令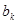 为
为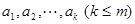 中最大值,称数列
中最大值,称数列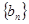 为
为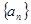 的“创新数列”.例如数列
的“创新数列”.例如数列 3,5,4,7的创新数列为3,5,5,7.
3,5,4,7的创新数列为3,5,5,7.考查自然数
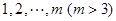 的所有排列,将每种排列都视为一个有穷数列
的所有排列,将每种排列都视为一个有穷数列 .
.(1)若
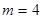 ,写出创新数列为3,4,4,4的所有数列
,写出创新数列为3,4,4,4的所有数列 ;
;(2)是否存在数列
 的创新数列为等比数列?若存在,求出符合条件的创新数列;若不存在,请说明理由.
的创新数列为等比数列?若存在,求出符合条件的创新数列;若不存在,请说明理由.(3)是否存在数列
 ,使它的创新数列为等差数列?若存在,求出满足所有条件的数列
,使它的创新数列为等差数列?若存在,求出满足所有条件的数列 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.解:(1)由题意,创新数列为3,4,4,4的所有数列 有两个,即3,4,1,2和
有两个,即3,4,1,2和
3,4,2,1. ……………(每写出一个给2分,多写不得分)4分
(2)存在数列 的创新数列为等比数列.……………………………………5分
的创新数列为等比数列.……………………………………5分
设数列 的创新数列为
的创新数列为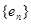 ,
,
因为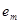 为前
为前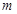 个自然数中最大的一个,所以
个自然数中最大的一个,所以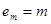 . ……………………6分
. ……………………6分
若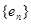 为等比数列,设公比为
为等比数列,设公比为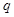 ,因为
,因为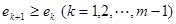 ,所以
,所以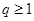 .…7分
.…7分
当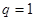 时,
时,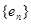 为常数列满足条件,即为数列
为常数列满足条件,即为数列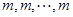
(或写通项公式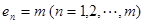 ); ……………………………………9分
); ……………………………………9分
当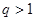 时,
时,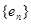 为增数列,符合条件的数列只能是
为增数列,符合条件的数列只能是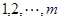 ,又
,又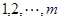 不满足等比数列.综上符合条件的创新数列只有一个. ……………………10分
不满足等比数列.综上符合条件的创新数列只有一个. ……………………10分
(3)存在数列 ,使它的创新数列为等差数列, ……………………11分
,使它的创新数列为等差数列, ……………………11分
设数列 的创新数列为
的创新数列为
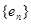 ,因为
,因为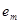 为前
为前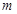 个自然数中最大的一个,所以
个自然数中最大的一个,所以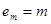 .
.
若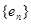 为等差数列,设公差为
为等差数列,设公差为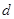 ,
,
因为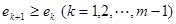 ,所以
,所以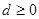 .且
.且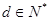 ……………………12分
……………………12分
当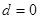 时,
时,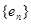 为常数列满足条件,即为数列
为常数列满足条件,即为数列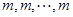 (或写通项公式
(或写通项公式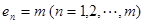 ),
),
此时数列 是首项为
是首项为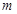 的任意一个排列,共有
的任意一个排列,共有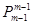 个数列; ……………14分
个数列; ……………14分
当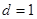 时,符合条件的数列
时,符合条件的数列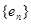 只能是
只能是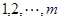 ,此时数列
,此时数列 是
是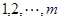 ,有1个; ……………………15分
,有1个; ……………………15分
当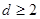 时,
时,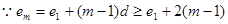
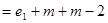 又
又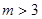

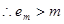 这与
这与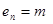 矛盾,所以此时
矛盾,所以此时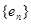 不存在。 …………17分
不存在。 …………17分
综上满足条件的数列 的个数为
的个数为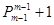 个(或回答
个(或回答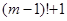 个). …………18分
个). …………18分
 有两个,即3,4,1,2和
有两个,即3,4,1,2和3,4,2,1. ……………(每写出一个给2分,多写不得分)4分
(2)存在数列
 的创新数列为等比数列.……………………………………5分
的创新数列为等比数列.……………………………………5分设数列
 的创新数列为
的创新数列为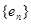 ,
,因为
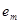 为前
为前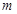 个自然数中最大的一个,所以
个自然数中最大的一个,所以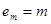 . ……………………6分
. ……………………6分若
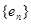 为等比数列,设公比为
为等比数列,设公比为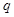 ,因为
,因为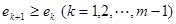 ,所以
,所以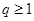 .…7分
.…7分当
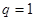 时,
时,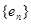 为常数列满足条件,即为数列
为常数列满足条件,即为数列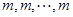
(或写通项公式
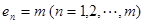 ); ……………………………………9分
); ……………………………………9分当
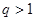 时,
时,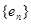 为增数列,符合条件的数列只能是
为增数列,符合条件的数列只能是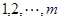 ,又
,又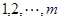 不满足等比数列.综上符合条件的创新数列只有一个. ……………………10分
不满足等比数列.综上符合条件的创新数列只有一个. ……………………10分(3)存在数列
 ,使它的创新数列为等差数列, ……………………11分
,使它的创新数列为等差数列, ……………………11分设数列
 的创新数列为
的创新数列为
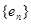 ,因为
,因为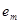 为前
为前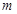 个自然数中最大的一个,所以
个自然数中最大的一个,所以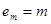 .
.若
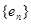 为等差数列,设公差为
为等差数列,设公差为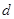 ,
,因为
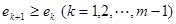 ,所以
,所以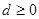 .且
.且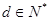 ……………………12分
……………………12分当
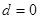 时,
时,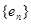 为常数列满足条件,即为数列
为常数列满足条件,即为数列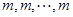 (或写通项公式
(或写通项公式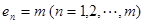 ),
),此时数列
 是首项为
是首项为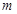 的任意一个排列,共有
的任意一个排列,共有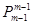 个数列; ……………14分
个数列; ……………14分当
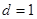 时,符合条件的数列
时,符合条件的数列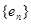 只能是
只能是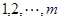 ,此时数列
,此时数列 是
是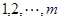 ,有1个; ……………………15分
,有1个; ……………………15分当
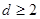 时,
时,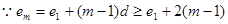
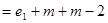 又
又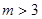

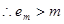 这与
这与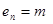 矛盾,所以此时
矛盾,所以此时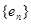 不存在。 …………17分
不存在。 …………17分综上满足条件的数列
 的个数为
的个数为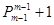 个(或回答
个(或回答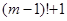 个). …………18分
个). …………18分略

练习册系列答案
相关题目

 的前
的前 项和为
项和为 ,且
,且 ;数列
;数列 为等差数列,且
为等差数列,且 ,
,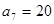 .
. ,
, 为数列
为数列 的前
的前 .
. 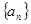 满足:
满足: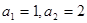 ,
,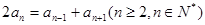 ,数列
,数列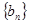 满足
满足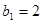 ,
,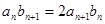 .
.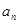 ;
; 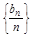 为等比数列;并求数列
为等比数列;并求数列 满足:
满足: ,
, ,
, .
. 及
及 (n
(n N*),求数列
N*),求数列 的前n项和
的前n项和 .
.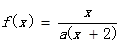 方程f(x)=x有唯一的解,
方程f(x)=x有唯一的解,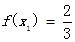
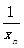 }是等差数列;
}是等差数列;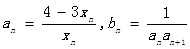 ,求sn=b1+b2+b3+…+bn;
,求sn=b1+b2+b3+…+bn;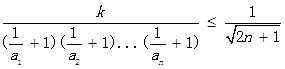 对一切n∈N﹡
对一切n∈N﹡ :
: 、
、 、
、 且
且 (
( ),与数列
),与数列 :
: 、
、 、
、 、
、 且
且 (
( .
. ,求
,求 的值;
的值; 的值,并求证当
的值,并求证当 ;
; ,且存在正整数
,且存在正整数 ,使得在
,使得在 ,
, ,
, ,
, 中有4项为100。求
中有4项为100。求 =
=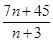 ,则
,则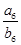 =________.
=________.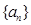 的各项均不为零,且公差
的各项均不为零,且公差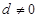 ,若
,若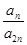 是一个与
是一个与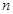 无关的常数
无关的常数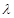 ,
, .
.