题目内容
(本题满分13分)设函数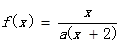 方程f(x)=x有唯一的解,
方程f(x)=x有唯一的解,
已知f(xn)=xn+1(n∈N﹡)且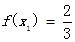
(1)求证:数列{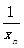 }是等差数列;
}是等差数列;
(2)若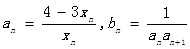 ,求sn=b1+b2+b3+…+bn;
,求sn=b1+b2+b3+…+bn;
(3)在(2)的冬件下,若不等式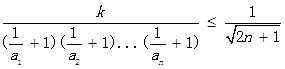 对一切n∈N﹡
对一切n∈N﹡
均成立,求k的最大值.
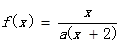 方程f(x)=x有唯一的解,
方程f(x)=x有唯一的解,已知f(xn)=xn+1(n∈N﹡)且
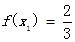
(1)求证:数列{
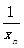 }是等差数列;
}是等差数列;(2)若
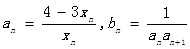 ,求sn=b1+b2+b3+…+bn;
,求sn=b1+b2+b3+…+bn;(3)在(2)的冬件下,若不等式
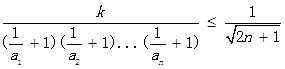 对一切n∈N﹡
对一切n∈N﹡均成立,求k的最大值.
解:(1)证明:由题意得: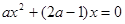
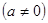 有唯一解,得
有唯一解,得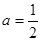
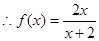 ,
,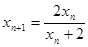
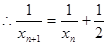 ,即
,即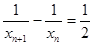
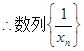 为等差数列 4分
为等差数列 4分
(2)又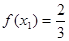 ,即
,即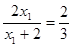 ,解得
,解得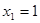
故 ,即
,即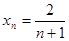
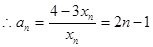 ,
,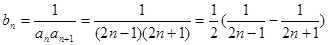
 8分
8分
(3)(理)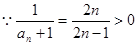
故原不等式即为对一切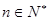 ,不等式
,不等式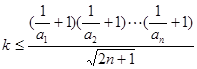 恒成立,
恒成立,
设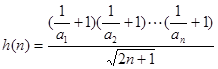 ,易知
,易知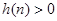
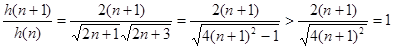
即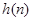 随
随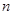 递增,故
递增,故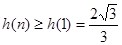 ,
,
所以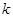 的最大值为
的最大值为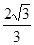 13分
13分
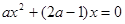
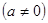 有唯一解,得
有唯一解,得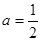
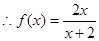 ,
,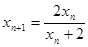
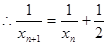 ,即
,即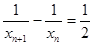
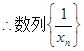 为等差数列 4分
为等差数列 4分(2)又
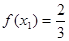 ,即
,即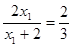 ,解得
,解得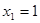
故
 ,即
,即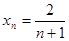
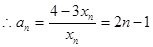 ,
,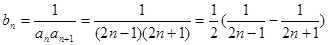
 8分
8分(3)(理)
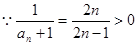
故原不等式即为对一切
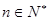 ,不等式
,不等式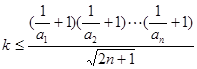 恒成立,
恒成立,设
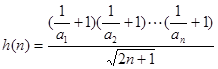 ,易知
,易知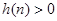
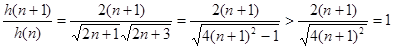
即
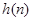 随
随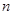 递增,故
递增,故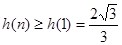 ,
,所以
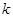 的最大值为
的最大值为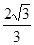 13分
13分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
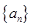 是公差为正数的等差数列,若
是公差为正数的等差数列,若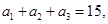
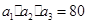 ,
,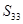 。
。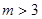 ,对于项数为
,对于项数为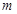 的有穷数列
的有穷数列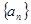 ,令
,令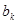 为
为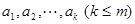 中最大值,称数列
中最大值,称数列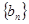 为
为 3,5,4,7的创新数列为3,5,5,7.
3,5,4,7的创新数列为3,5,5,7.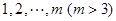 的所有排列,将每种排列都视为一个有穷数列
的所有排列,将每种排列都视为一个有穷数列 .
.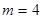 ,写出创新数列为3,4,4,4的所有数列
,写出创新数列为3,4,4,4的所有数列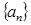 的前n项和为
的前n项和为 ,
,
 是等差数列,并求
是等差数列,并求 ,求证:
,求证: .
. 成等差数列,点
成等差数列,点 是函数
是函数 图像上任意一点,点
图像上任意一点,点 的轨迹是函数
的轨迹是函数 的图像
的图像 的不等式
的不等式
 时,总有
时,总有 恒成立,求
恒成立,求 的取值范围
的取值范围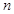 名同学在玩一个数字哈哈镜游戏,这些同学依次编号为
名同学在玩一个数字哈哈镜游戏,这些同学依次编号为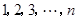 .在哈哈镜中,每个同学看到的像用数对
.在哈哈镜中,每个同学看到的像用数对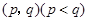 表示,规则如下:若编号为
表示,规则如下:若编号为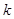 的同学看到像为
的同学看到像为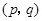 ,则编号为
,则编号为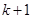 的同学看到像为
的同学看到像为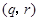 ,且
,且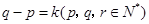 .已知编号为1的同学看到的像为
.已知编号为1的同学看到的像为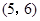 .请根据以上规律,编号为3和
.请根据以上规律,编号为3和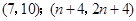

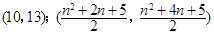

 ,定义向量
,定义向量 。下列命题中真命题是
。下列命题中真命题是



 的前
的前 项和为
项和为 ,且
,且 为确定的常数,则下列各式中,也为确定的常数是( )
为确定的常数,则下列各式中,也为确定的常数是( )



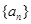 的前n项和
的前n项和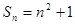 ,则
,则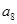 的值为
的值为