题目内容
已知正项数列{an},其前n项和Sn满足10Sn=an2+5an+6且a1,a3,a15成等比数列,求数列{an}的通项an

∵10Sn=an2+5an+6, ①
∴10a1=a12+5a1+6,解之得a1=2或a1=3 —————————————— 2分
—————————————— 2分
又10Sn-1=an-12+5an-1+6(n≥2),②
由①-②得 10an=(an2-an-12)+6(an-an-1),即(an+an-1)(an-an-1-5)="0 "
∵an+an-1>0 , ∴an-an-1="5" (n≥2) -------------------------------6分
-------------------------------6分
当a1=3时,a3=13,a15=73 a1, a3,a15不成等比数列∴a1≠3;-----------8分
a1, a3,a15不成等比数列∴a1≠3;-----------8分
当a1=2时, a3=12, a15=72, 有 a32=a1a15, ∴a1=2, ∴an=5n-3
∴10a1=a12+5a1+6,解之得a1=2或a1=3
 —————————————— 2分
—————————————— 2分又10Sn-1=an-12+5an-1+6(n≥2),②
由①-②得 10an=(an2-an-12)+6(an-an-1),即(an+an-1)(an-an-1-5)="0 "
∵an+an-1>0 , ∴an-an-1="5" (n≥2)
 -------------------------------6分
-------------------------------6分当a1=3时,a3=13,a15=73
 a1, a3,a15不成等比数列∴a1≠3;-----------8分
a1, a3,a15不成等比数列∴a1≠3;-----------8分当a1=2时, a3=12, a15=72, 有 a32=a1a15, ∴a1=2, ∴an=5n-3

略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
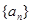 的前
的前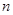 项和为
项和为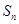 ,已知
,已知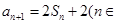 N
N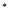 ).
). 求数列
求数列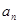 与
与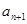 之间插入n个数,使这n+2个数组成公差为
之间插入n个数,使这n+2个数组成公差为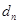 的等差数列,求数列
的等差数列,求数列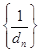 的前
的前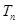 .
.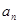 }的前n 项和为
}的前n 项和为 ,已知
,已知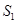 ,
,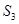 ,
,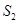 成等差数列
成等差数列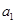 -
-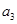 =3,求
=3,求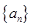 是公差为正数的等差数列,若
是公差为正数的等差数列,若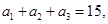
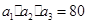 ,
,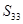 。
。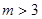 ,对于项数为
,对于项数为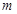 的有穷数列
的有穷数列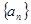 ,令
,令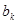 为
为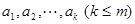 中最大值,称数列
中最大值,称数列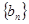 为
为 3,5,4,7的创新数列为3,5,5,7.
3,5,4,7的创新数列为3,5,5,7.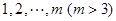 的所有排列,将每种排列都视为一个有穷数列
的所有排列,将每种排列都视为一个有穷数列 .
.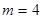 ,写出创新数列为3,4,4,4的所有数列
,写出创新数列为3,4,4,4的所有数列 ,定义向量
,定义向量 。下列命题中真命题是
。下列命题中真命题是



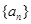 的前n项和
的前n项和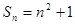 ,则
,则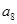 的值为
的值为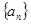 是等差数列,且
是等差数列,且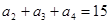 ,则这个数列的前5项和
,则这个数列的前5项和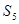 =()
=() ,则
,则 .
.