题目内容
10.已知实数x,y,z满足x+y+z=1,则x2+y2+z2的最小值为$\frac{1}{3}$.分析 利用条件x+y+z=1,构造柯西不等式(x+y+z)2≤(x2+y2+z2)(12+12+12)进行解题即可.
解答 解:由柯西不等式可知:(x+y+z)2≤(x2+y2+z2)(12+12+12)
故x2+y2+z2≥$\frac{1}{3}$,即:x2+2y2+3z2的最小值为$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题主要考查了函数的最值,以及柯西不等式的应用,解题的关键是利用(x+y+z)2≤(x2+y2+z2)(12+12+12)进行解决.

练习册系列答案
相关题目
15.已知集合A={y|y=x2+2x-3},$B=\left\{{\left.y\right|y=x+\frac{1}{x},x>0}\right\}$,则有( )
| A. | A⊆B | B. | B⊆A | C. | A=B | D. | A∩B=φ |
2.函数f(x)=$\sqrt{3}$x+2cosx在区间[0,$\frac{π}{2}$]上的最大值是( )
| A. | 2 | B. | $\frac{\sqrt{3}π}{2}$ | C. | $\frac{\sqrt{3}π+3}{3}$ | D. | 1 |
19.已知过点(-2,3)可以作圆(x-a)2+(y-2)2=9的两条切线,则a的范围是( )
| A. | (-∞,-3)∪(3,+∞) | B. | $(-∞,-2-2\sqrt{2})∪(-2+2\sqrt{2},+∞)$ | ||
| C. | (-3,3) | D. | $(-2-2\sqrt{2},-2+2\sqrt{2})$ |
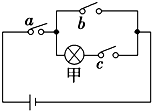 如图所示的电路有a,b,c三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且是相互独立的,则灯泡甲亮的概率为$\frac{1}{8}$.
如图所示的电路有a,b,c三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且是相互独立的,则灯泡甲亮的概率为$\frac{1}{8}$. 如图所示,已知半圆的直径AB=6cm,CD是半圆上长为2cm的弦,问:当弦CD在半圆上滑动时,AC和BD延长线的夹角是定值吗?若是,试求出这个定角的正弦值;若不是,请说明理由.
如图所示,已知半圆的直径AB=6cm,CD是半圆上长为2cm的弦,问:当弦CD在半圆上滑动时,AC和BD延长线的夹角是定值吗?若是,试求出这个定角的正弦值;若不是,请说明理由.