题目内容
8.已知$\overrightarrow{a}$=(2cosα,2sinα),$\overrightarrow{b}$=(cosβ,sinβ),0<α<β<2π.(1)若$\overrightarrow{c}$=(1,1),且$\overrightarrow{a}$∥$\overrightarrow{c}$,求$\overrightarrow{a}$的值;
(2)若$\overrightarrow{a}$•$\overrightarrow{b}$=1,cos(α+β)=$\frac{1}{3}$,求tanαtanβ的值;
(3)设$\overrightarrow{c}$=(2,0),若$\overrightarrow{a}$+2$\overrightarrow{b}$=$\overrightarrow{c}$,求α-β的值.
分析 (1)根据平面向量共线的坐标表示,列出方程求出α的值,即可得出向量$\overrightarrow{a}$;
(2)根据平面向量的数量积与三角恒等变换,列出方程组,求出tanαtanβ的值;
(3)根据平面向量的坐标运算,结合三角恒等变换与角的取值范围,求出α-β的值.
解答 解:(1)∵$\overrightarrow{a}$=(2cosα,2sinα),$\overrightarrow{b}$=(cosβ,sinβ),0<α<β<2π.
$\overrightarrow{c}$=(1,1),且$\overrightarrow{a}$∥$\overrightarrow{c}$,
∴2cosα•1-2sinα•1=0,
即sinα=cosα,
∴α=$\frac{π}{4}$或$\frac{5π}{4}$,
∴$\overrightarrow{a}$=($\sqrt{2}$,$\sqrt{2}$)或$\overrightarrow{a}$=(-$\sqrt{2}$,-$\sqrt{2}$);
(2)∵$\overrightarrow{a}$•$\overrightarrow{b}$=1,cos(α+β)=$\frac{1}{3}$,
∴2cosαcosβ+2sinαsinβ=1,
即cosαcosβ+sinαsinβ=$\frac{1}{2}$①,
又cosαcosβ-sinαsinβ=$\frac{1}{3}$②,
由①②组成方程组,求出sinαsinβ=$\frac{1}{12}$,cosαcosβ=$\frac{5}{12}$,
∴tanαtanβ=$\frac{sinαsinβ}{cosαcosβ}$=$\frac{\frac{1}{12}}{\frac{5}{12}}$=$\frac{1}{5}$;
(3)$\overrightarrow{c}$=(2,0),$\overrightarrow{a}$+2$\overrightarrow{b}$=$\overrightarrow{c}$,
$\overrightarrow{a}$+2$\overrightarrow{b}$=(2cosα+2cosβ,2sinα+2sinβ),
∴$\left\{\begin{array}{l}{2cosα+2cosβ=2}\\{2sinα+2sinβ=0}\end{array}\right.$,
即$\left\{\begin{array}{l}{cosα+cosβ=1}\\{sinα+sinβ=0}\end{array}\right.$,
∴cos2α+sin2α=1-2cosβ+cos2β+sin2β=2-2cosβ=1,
解得cosβ=$\frac{1}{2}$,cosα=$\frac{1}{2}$;
又∵0<α<β<2π,
∴sinα=$\frac{\sqrt{3}}{2}$,sinβ=-$\frac{\sqrt{3}}{2}$;
∴α=$\frac{π}{3}$,β=$\frac{5π}{3}$,α-β=-$\frac{4π}{3}$.
点评 本题考查了平面向量的坐标运算问题,也考查了三角函数的恒等变换与求值运算问题,是综合性题目.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案| A. | 0 | B. | 3 | C. | 6 | D. | 9 |
| A. | 圆柱的侧面展开图是一个矩形 | |
| B. | 圆锥中过圆锥轴的截面是一个等腰三角形 | |
| C. | 直角三角形绕它的一边旋转一周而形成的曲面所围成的几何体是一个圆锥 | |
| D. | 用一个平面截一个圆柱,所得截面可能是矩形 |
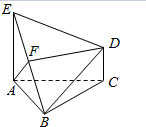 如图,△ABC为正三角形,AE和CD都垂直于平而ABC,F是BE中点,AE=AB=2,CD=1.
如图,△ABC为正三角形,AE和CD都垂直于平而ABC,F是BE中点,AE=AB=2,CD=1.