题目内容
20.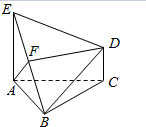 如图,△ABC为正三角形,AE和CD都垂直于平而ABC,F是BE中点,AE=AB=2,CD=1.
如图,△ABC为正三角形,AE和CD都垂直于平而ABC,F是BE中点,AE=AB=2,CD=1.(1)求证:DF∥平面ABC;
(2)求证:AF⊥DE;
(3)求异面直线AF与BC所成角的余弦值.
分析 (1)取AC中点O,过O作平面ABC的垂线交DE,连结OB,以O为原点,OB、OC、OG所在直线分别为x、y、z轴,建立空间直角坐标系,利用向量法能证明DF∥平面ABC.
(2)分别求出$\overrightarrow{AF}$,$\overrightarrow{DE}$,利用向量法能证明AF⊥DE.
(3)分别求出$\overrightarrow{AF}$,$\overrightarrow{BC}$,利用向量法能求出异面直线AF与BC所成角的余弦值.
解答 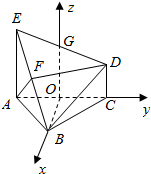 (1)证明:取AC中点O,过O作平面ABC的垂线交DE
(1)证明:取AC中点O,过O作平面ABC的垂线交DE
连结OB,则OG⊥OB,OG⊥OC,
∵△ABC是正三角形,O是AC中点,∴OB⊥OC,
以O为原点,OB、OC、OG所在直线分别为x、y、z轴,建立空间直角坐标系,
∵F是BE中点,AE=AB=2,CD=1,
∴A(0,-1,0),B($\sqrt{3},0,0$),C(0,1,0),
D(0,1,1),E(0,-1,2),F($\frac{\sqrt{3}}{2},-\frac{1}{2},1$),
∴$\overrightarrow{DF}$=($\frac{\sqrt{3}}{2},-\frac{3}{2}$,0),$\overrightarrow{AF}$=($\frac{\sqrt{3}}{2},\frac{1}{2},1$),$\overrightarrow{DE}$=(0,-2,1),
$\overrightarrow{BC}$=(-$\sqrt{3}$,1,0),$\overrightarrow{CD}$=(0,0,1),
∵CD⊥平面ABC,∴$\overrightarrow{CD}$=(0,0,1)是平面ABC的一个法向量,
∵$\overrightarrow{DF}•\overrightarrow{CD}$=$\frac{\sqrt{3}}{2}×0+(-\frac{3}{2})×0+0×1=0$,∴$\overrightarrow{DF}⊥\overrightarrow{CD}$,
又DF?平面ABC,∴DF∥平面ABC.
(2)证明:∵$\overrightarrow{AF}$=($\frac{\sqrt{3}}{2},\frac{1}{2},1$),$\overrightarrow{DE}$=(0,-2,1),
∴$\overrightarrow{AF}•\overrightarrow{DE}$=0-1+1=0,
∴AF⊥DE.
(3)解:∵$\overrightarrow{AF}$=($\frac{\sqrt{3}}{2},\frac{1}{2},1$),$\overrightarrow{BC}$=(-$\sqrt{3}$,1,0),
设AF、BC所成角为θ,
cosθ=|$\frac{\overrightarrow{AF}•\overrightarrow{BC}}{|\overrightarrow{AF}|•|\overrightarrow{BC}|}$|=|$\frac{-\frac{3}{2}+\frac{1}{2}}{\sqrt{2}•2}$|=$\frac{\sqrt{2}}{4}$.
∴异面直线AF与BC所成角的余弦值$\frac{\sqrt{2}}{4}$.
点评 本题考查线面平行的证明,考查异面直线垂直的证明,考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案| A. | $\overrightarrow{CN}$ | B. | $\overrightarrow{BC}$ | C. | $\overrightarrow{C{C}_{1}}$ | D. | $\overrightarrow{{B}{C}_{1}}$ |
| A. | 10 | B. | -10 | C. | -14 | D. | 14 |
| A. | [-2,2] | B. | [-$\frac{5}{2}$,$\frac{5}{2}$] | C. | (-2,2) | D. | (-$\frac{5}{2}$,$\frac{5}{2}$) |