题目内容
18.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)过点A($\sqrt{14}$,$\sqrt{5}$),且点A到双曲线的两条渐近线的距离的积为$\frac{4}{3}$,求此双曲线方程.分析 由题意,双曲线的渐近线的方程为bx±ay=0,利用点A到双曲线的两条渐近线的距离的积为$\frac{4}{3}$,求出a,b的关系,再利用双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)过点A($\sqrt{14}$,$\sqrt{5}$),求出a,b,即可求此双曲线方程.
解答 解:由题意,双曲线的渐近线的方程为bx±ay=0,
∵点A到双曲线的两条渐近线的距离的积为$\frac{4}{3}$,
∴$\frac{14{b}^{2}-5{a}^{2}}{{b}^{2}+{a}^{2}}$=$\frac{4}{3}$,
∴a=$\sqrt{2}b$,
∴双曲线方程为$\frac{{x}^{2}}{2{b}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,
∵过点A($\sqrt{14}$,$\sqrt{5}$),
∴$\frac{14}{2{b}^{2}}-\frac{5}{{b}^{2}}$=1,
∴b=$\sqrt{2}$,
∴a=2,
∴双曲线方程为$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{2}=1$.
点评 本题考查双曲线的方程,考查点到直线的距离公式,考查学生的计算能力,比较基础.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案
相关题目
9.二项式(x3-$\frac{1}{{x}^{2}}$)5的展开式中的常数项为( )
| A. | 10 | B. | -10 | C. | -14 | D. | 14 |
6.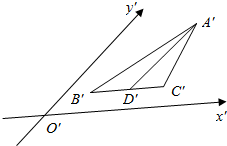 如图所示的水平放置的三角形的直观图中,D′是△A′B′C′中B′C′边的中点,那么A′B′,A′D′,A′C′三条线段对应原图形中线段AB,AD,AC中( )
如图所示的水平放置的三角形的直观图中,D′是△A′B′C′中B′C′边的中点,那么A′B′,A′D′,A′C′三条线段对应原图形中线段AB,AD,AC中( )
 如图所示的水平放置的三角形的直观图中,D′是△A′B′C′中B′C′边的中点,那么A′B′,A′D′,A′C′三条线段对应原图形中线段AB,AD,AC中( )
如图所示的水平放置的三角形的直观图中,D′是△A′B′C′中B′C′边的中点,那么A′B′,A′D′,A′C′三条线段对应原图形中线段AB,AD,AC中( )| A. | 最长的是AB,最短的是AC | B. | 最长的是AC,最短的是AB | ||
| C. | 最长的是AB,最短的是AD | D. | 最长的是AD,最短的是AC |
10.已知非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|且|$\overrightarrow{a}$+2$\overrightarrow{b}$|>|m$\overrightarrow{b}$|恒成立,则实数m的取值范围是( )
| A. | [-2,2] | B. | [-$\frac{5}{2}$,$\frac{5}{2}$] | C. | (-2,2) | D. | (-$\frac{5}{2}$,$\frac{5}{2}$) |