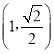题目内容
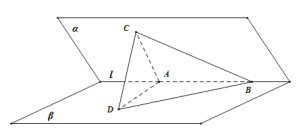
【题目】如图，海岸公路MN的北方有一个小岛A（大小忽略不计）盛产海产品，在公路MN的B处有一个海产品集散中心，点C在B的正西方向10
处，
，
，计划开辟一条运输线将小岛的海产品运送到集散中心.现有两种方案：①沿线段AB开辟海上航线：②在海岸公路MN上选一点P建一个码头，先从海上运到码头，再公路MN运送到集散中心.已知海上运输、岸上运输费用分别为400元/、200元/.
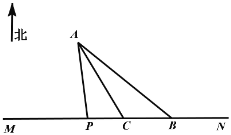
（1）求方案①的运输费用；
（2）请确定P点的位置，使得按方案②运送时运输费用最低？
【答案】（1）20000元；（2）P在点B正西方向
千米.
【解析】
（1）利用正弦定理求得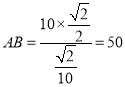
，即可求得费用；
（2）设
，总费用
，
利用导函数求解最值即可得解.
（1）
，在钝角三角形ABC中，
，
，
由正弦定理可得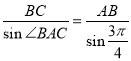
，，
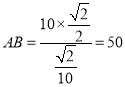所以方案①的运输费用为400×50=20000元；
（2）由（1）可得点A到公路所在直线的距离为
，设，
易得
则总费用，
，
，，
当
，
所以
，单调递减，
，单调递增，
所以当
时，
取得最小值为
，
此时
.
所以P在点B正西方向千米.
练习册系列答案
相关题目
【题目】某高校在
年的自主招生考试成绩中随机抽取
名学生的笔试成绩，按成绩共分五组，得到如下的频率分布表：
组号 | 分组 | 频数 | 频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
（1）请写出频率分布表中
、
、
的值，若同组中的每个数据用该组区间的中间值代替，请估计全体考生的平均成绩；
（2）为了能选出最优秀的学生，高校决定在笔试成绩高的第
、
、
组中用分层抽样的方法抽取
名考生进入第二轮面试，求第、、组中每组各抽取多少名考生进入第二轮的面试；
（3）在（2）的前提下，学校要求每个学生需从
、
两个问题中任选一题作为面试题目，求第三组和第五组中恰好有
个学生选到问题的概率．
