Question

【题目】已知F1，F2为椭圆C：的左、右焦点，椭圆C过点M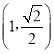，且MF2⊥F1F2.

（1）求椭圆C的方程；

（2）经过点P（2，0）的直线交椭圆C于A，B两点，若存在点Q（m，0），使得|QA|＝|QB|.

①求实数m的取值范围：

②若线段F1A的垂直平分线过点Q，求实数m的值.

Answer 1

【答案】（1）y2＝1（2）①m∈[0，）②

【解析】

（1）由椭圆过M点，及且MF2⊥F1F2，可得c＝1，求得a，b的值，求出椭圆的方程；

（2）①设直线AB的方程与椭圆联立，求出两根之和，可得AB的中点N的坐标，由|QA|＝|QB|.可得直线AB⊥QN，可得斜率之积为﹣1，可得m的表达式m，进而可得m的范围；

②由题意|QF1|＝|QA|＝QB|，在以为原心，为半径的圆上，再与椭圆方程联立，由根与系数的关系列式化简，求出m的值.

解：（1）因为椭圆过M（1，），MF2⊥F1F2，

所以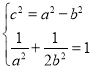解得：a2＝2，b2＝1，所以椭圆的方程为：y2＝1；

（2）设直线的方程为：y＝k（x﹣2），

代入椭圆的方程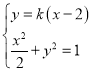，整理可得：（1+2k2）x2﹣8k2x+8k2﹣2＝0，

因为直线l与椭圆C由两个交点，所以＝64k4﹣4（1+2k2）（8k2﹣2）＞0，

解得2k2＜1；

设A（x1，y1），B（x2，y2），则有x1+x2，x1x2，

①设AB中点为M（x0，y0），

则有x0，y0＝k（x0﹣2），

当k≠0时，因为|QA|＝|QB|，∴QM⊥l，

∴kQMk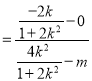k＝﹣1，解得m，

∴m1∈（0，），

当k＝0，可得m＝0，

综上所述：m∈[0，）.

②由题意|QF1|＝|QA|＝QB|，且F1（﹣1，0），

由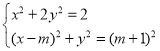，整理可得：x2﹣4mx﹣4m＝0，

所以x1，x2也是此方程的两个根，所以x1+x2＝4m，x1x2＝﹣4m，

所以，解得k2，所以m.

所以m的值为.