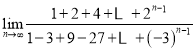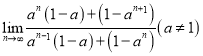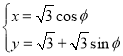题目内容
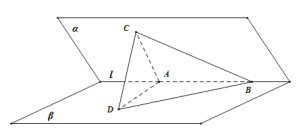
【题目】如图，二面角α﹣1﹣β的平面角的大小为60°，A，B是1上的两个定点，且AB＝2．C∈α，D∈β，满足AB与平面BCD所成的角为30°，且点A在平面BCD上的射影H在△BCD的内部（包括边界），则点H的轨迹的长度等于（ ）
A.
B.
C.
D.
【答案】A
【解析】
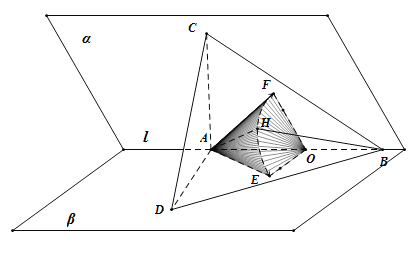
根据题意：点H的轨迹是以点B为球心，以
为半径的球与以AB为轴，母线AH与轴AB成60°的圆锥侧面交线的一部分，该部分是圆心角为
的弧长，只要求出半径即可.
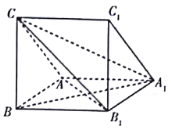
如图所示：
因为AB与平面BCD所成的角为30°，且点A在平面BCD上的射影H， AB＝2，
所以
，
所以点H在以点B为球心，以
为半径的球面上，
又点H在以AB为轴，以AH为母线的圆锥的侧面上，
所以点H的轨迹为以点B为球心，以为半径的球与以AB为轴，母线AH与轴AB成60°的圆锥侧面交线的一部分，
即图中扇形EOF的弧EF，且扇形所在平面垂直于AB，
因为二面角α﹣1﹣β的平面角的大小为60°，
所以∠EOF=60°，
又
，
所以点H的轨迹的长度等于
，
故选：A
练习册系列答案
阅读快车系列答案
相关题目
【题目】某单位在2019年重阳节组织50名退休职工（男、女各25名）旅游,退休职工可以选择到甲、乙两个景点其中一个去旅游.他们最终选择的景点的结果如下表：
男性 | 女性 | |
甲景点 | 20 | 10 |
乙景点 | 5 | 15 |
（1）据此资料分析,是否有
的把握认为选择哪个景点与性别有关？
（2）按照游览不同景点用分层抽样的方法,在女职工中选取5人,再从这5人中随机抽取2人进行采访,求这2人游览的景点不同的概率.
附：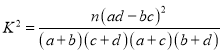
,
.
P（ | 0.010 | 0.005 | 0.001 |
k | 6.635 | 7.879 | 10.828 |
