题目内容
【题目】在平面直角坐标系
中，P为直线
：
上的动点，动点Q满足
，且原点O在以
为直径的圆上.记动点Q的轨迹为曲线C
（1）求曲线C的方程：
（2）过点
的直线
与曲线C交于A，B两点，点D（异于A，B）在C上，直线
，
分别与x轴交于点M，N，且
，求
面积的最小值.
【答案】（1）
（2）
【解析】
（1）设动点
，表示出
，再由原点O在以
为直径的圆上，转化为
，得到曲线C的方程.
（2）设而不解，利用方程思想、韦达定理构建
面积的函数关系式，再求最小值.
解：（1）由题意，不妨设，则
，
，
∵O在以为直径的圆上，∴，∴
，
∴，∴曲线C的方程为.
（2）设
，
，
，
，
，
依题意，可设
：
（其中
），由方程组
消去x并整理，得
，则
，
，
同理可设
，
，
可得
，
，
∴
，
，
又∵
，∴
，
∴
，∴
，
∴
，
∴
，
∴当
时，面积取得最小值，其最小值为.
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
【题目】某单位在2019年重阳节组织50名退休职工（男、女各25名）旅游,退休职工可以选择到甲、乙两个景点其中一个去旅游.他们最终选择的景点的结果如下表：
男性 | 女性 | |
甲景点 | 20 | 10 |
乙景点 | 5 | 15 |
（1）据此资料分析,是否有
的把握认为选择哪个景点与性别有关？
（2）按照游览不同景点用分层抽样的方法,在女职工中选取5人,再从这5人中随机抽取2人进行采访,求这2人游览的景点不同的概率.
附：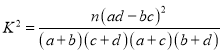
,
.
P（ | 0.010 | 0.005 | 0.001 |
k | 6.635 | 7.879 | 10.828 |
