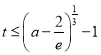题目内容
【题目】对一个量用两种方法分别算一次,由结果相同而构造等式,这种方法称为“算两次”的思想方法.利用这种方法,结合二项式定理,可以得到很多有趣的组合恒等式.
(1)根据恒等式![]() 两边
两边![]() 的系数相同直接写出一个恒等式,其中
的系数相同直接写出一个恒等式,其中![]() ;
;
(2)设![]() ,利用上述恒等式证明:
,利用上述恒等式证明:![]() .
.
【答案】(1)![]() ,其中
,其中![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)利用二项式定理系数的性质,左右两边分别表示出![]() 的系数即可.
的系数即可.
(2)证明左边等于右边,用上![]() ,
,![]() ,
,![]() ,(1)的结果以及
,(1)的结果以及![]() 逐步推证即可.
逐步推证即可.
解:(1)![]() ,
,
等式左边![]() 的系数为
的系数为![]() ,
,
右边![]() 的系数这样产生:
的系数这样产生:
![]() 中的1与
中的1与![]() 中的
中的![]() 的系数的
的系数的![]() 的积,即
的积,即![]() ,
,
![]() 中
中![]() 的系数
的系数![]() 与
与![]() 中
中![]() 的系数的
的系数的![]() 的积,即
的积,即![]() ,
,
![]() 中
中![]() 的系数
的系数![]() 与
与![]() 中
中![]() 的系数的
的系数的![]() 的积,即
的积,即![]() ,
,
![]() 中
中![]() 的系数
的系数![]() 与
与![]() 中
中![]() 的系数的
的系数的![]() 的积,即
的积,即![]() ,
,
![]()
![]() 中
中![]() 的系数
的系数![]() 与
与![]() 中
中![]() 的系数的
的系数的![]() 的积,即
的积,即![]() ,
,
所以![]() .
.
(2)当![]() ,且
,且![]() 时,
时,![]() ,
,
由(1)得![]()
左边=![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 右边,
右边,
所以![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
【题目】随着我国经济结构调整和方式转变,社会对高质量人才的需求越来越大,因此考研现象在我国不断升温.某大学一学院甲、乙两个本科专业,研究生的报考和录取情况如下表,则
性别 | 甲专业报考人数 | 乙专业报考人数 | 性别 | 甲专业录取率 | 乙专业录取率 | |
男 | 100 | 400 | 男 |
|
| |
女 | 300 | 100 | 女 |
|
|
A.甲专业比乙专业的录取率高B.乙专业比甲专业的录取率高
C.男生比女生的录取率高D.女生比男生的录取率高