题目内容

椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率e=
3
2
，a+b=3．
（1）求椭圆C的方程；
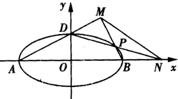
（2）如图，A，B，D是椭圆C的顶点，P是椭圆C上除顶点外的任意点，直线DP交x轴于点N直线AD交BP于点M，设BP的斜率为k，MN的斜率为m，证明2m-k为定值．
（1）因为e=
c
a
=
3
2
，所以
c2
a2
=
a2-b2
a2
=
3
4
，即a2=4b2，a=2b．
又a+b=3，得a=2，b=1．
所以椭圆C的方程为
x2
4
+y2=1；
（2）证明：因为B（2，0），P不为椭圆顶点，则可设直线BP的方程为y=k(x-2)(k≠0，k≠±
1
2
)．
联立
y=k(x-2)
x2
4
+y2=1
，得（4k2+1）x2-16k2x+16k2-4=0．
所以xP+2=
16k2
4k2+1
，xP=
8k2-2
4k2+1
．
则yP=k(
8k2-2
4k2+1
-2)=
-4k
4k2+1
．
所以P（
8k2-2
4k2+1
，
-4k
4k2+1
）．
又直线AD的方程为y=
1
2
x+1．
联立
y=k(x-2)
y=
1
2
x+1
，解得M（
4k+2
2k-1
，
4k
2k-1
）．
由三点D（0，1），P（
8k2-2
4k2+1
，
-4k
4k2+1
），N（x，0）共线，
得
-4k
4k2+1
-1
8k2-2
4k2+1
-0
=
0-1
x-0
，所以N（
4k-2
2k+1
，0）．
所以MN的斜率为m=
4k
2k-1
-0
4k+2
2k-1
-
4k-2
2k+1
=
4k(2k+1)
2(2k+1)2-2(2k-1)2
=
2k+1
4
．
则2m-k=
2k+1
2
-k=
1
2
．
所以2m-k为定值
1
2
．
练习册系列答案
相关题目
已知抛物线C的顶点为O（0，0），焦点F（0，1）
（Ⅰ）求抛物线C的方程；
（Ⅱ）过F作直线交抛物线于A、B两点．若直线OA、OB分别交直线l：y=x-2于M、N两点，求|MN|的最小值．
如图，椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别为F1，F2，离心率e=
5
5
，过F1的直线交椭圆于M、N两点，且△MNF2周长为4
5
．
（Ⅰ）求椭圆E的方程；
（Ⅱ）已知过椭圆中心，且斜率为k（k≠0）的直线与椭圆交于A、B两点，P是线段AB的垂直平分线与椭圆E的一个交点，若△APB的面积为
40
9
，求k的值．
过点P（1，1）作直线与双曲线x2-
y2
2
=1交于A、B两点，使点P为AB中点，则这样的直线（　　）
A．存在一条，且方程为2x-y-1=0
B．存在无数条
C．存在两条，方程为2x±（y+1）=0
D．不存在
已知椭圆C1：
x2
a2
+
y2
b2
=1（a＞b＞0）与直线x+y-1=0相交于A、B两点．
（1）若椭圆的半焦距c=
3
，直线x=±a与y=±b围成的矩形ABCD的面积为8，求椭圆的方程；
（2）若O（
OA
•
OB
=0为坐标原点），求证：
1
a2
+
1
b2
=2；
（3）在（2）的条件下，若椭圆的离心率e满足
3
3
≤e≤
2
2
，求椭圆长轴长的取值范围．
已知抛物线C：y2=2px（p＞0）上横坐标为1的点M到抛物线C焦点F的距离|MF|=2．
（1）试求抛物线C的标准方程；
（2）若直线l与抛物线C相交所得的弦的中点为（2，1），试求直线l的方程．
已知抛物线C1：y2=8x与双曲线C2：
x2
a2
-
y2
b2
=1（a＞0，b＞0）有公共焦点F2，点A是曲线C1，C2在第一象限的交点，且|AF2|=5．
（1）求双曲线C2的方程；
（2）以双曲线C2的另一焦点F1为圆心的圆M与直线y=
3
x相切，圆N：（x-2）2+y2=1．过点P（1，
3
）作互相垂直且分别与圆M、圆N相交的直线l1和l2，设l1被圆M截得的弦长为s，l2被圆N截得的弦长为t，问：
s
t
是否为定值？如果是，请求出这个定值；如果不是，请说明理由．
已知双曲线C：x2-
y2
2
=1，过点P（-1，-2）的直线交C于A，B两点，且点P为线段AB的中点．
（1）求直线AB的方程；
（2）求弦长|AB|的值．
已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)过点(1，
q
2
)，且离心率e=
1
2
．
（Ⅰ）求椭圆方程；
（Ⅱ）若直线l：y=kx+m（k≠0）与椭圆交于不同的两点M、N，且线段MN的垂直平分线过定点G(
1
8
，0)，求k的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网