题目内容
已知椭圆C:
+
=1(a>b>0)过点(1,
),且离心率e=
.
(Ⅰ)求椭圆方程;
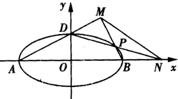
(Ⅱ)若直线l:y=kx+m(k≠0)与椭圆交于不同的两点M、N,且线段MN的垂直平分线过定点G(
,0),求k的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| q |
| 2 |
| 1 |
| 2 |
(Ⅰ)求椭圆方程;
(Ⅱ)若直线l:y=kx+m(k≠0)与椭圆交于不同的两点M、N,且线段MN的垂直平分线过定点G(
| 1 |
| 8 |
(Ⅰ)由题意椭圆的离心率∴e=
=
∴a=2c∴b2=a2-c2=3c2
∴椭圆方程为
+
=1又点(1,
)在椭圆上∴
+
=1∴c2=1
∴椭圆的方程为
+
=1…(4分)
(Ⅱ)设M(x1,y1),N(x2,y2)由
消去y并整理得(3+4k2)x2+8kmx+4m2-12=0…(6分)
∵直线y=kx+m与椭圆有两个交点△=(8km)2-4(3+4k2)(4m2-12)>0,即m2<4k2+3…(8分)
又x1+x2=-
∴MN中点P的坐标为(-
,
)…(9分)
设MN的垂直平分线l'方程:y=-
(x-
)
∵p在l'上∴
=-
(-
-
)即4k2+8km+3=0
∴m=-
(4k2+3)…(11分)
将上式代入得
<4k2+3
∴k2>
即k>
或k<-
,∴k的取值范围为(-∞,-
)∪(
,+∞)
| c |
| a |
| 1 |
| 2 |
∴椭圆方程为
| x2 |
| 4c2 |
| y2 |
| 3c2 |
| 3 |
| 2 |
| 1 |
| 4c2 |
(
| ||
| 3c2 |
∴椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)设M(x1,y1),N(x2,y2)由
|
消去y并整理得(3+4k2)x2+8kmx+4m2-12=0…(6分)
∵直线y=kx+m与椭圆有两个交点△=(8km)2-4(3+4k2)(4m2-12)>0,即m2<4k2+3…(8分)
又x1+x2=-
| 8km |
| 3+4k2 |
| 4km |
| 3+4k2 |
| 3m |
| 3+4k2 |
设MN的垂直平分线l'方程:y=-
| 1 |
| k |
| 1 |
| 8 |
∵p在l'上∴
| 3m |
| 3+4k2 |
| 1 |
| k |
| 4km |
| 3+4k2 |
| 1 |
| 8 |
∴m=-
| 1 |
| 8k |
将上式代入得
| (4k2+3)2 |
| 64k2 |
∴k2>
| 1 |
| 20 |
即k>
| ||
| 10 |
| ||
| 10 |
| ||
| 10 |
| ||
| 10 |

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目