题目内容
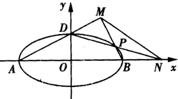
如图,椭圆E:
+
=1(a>b>0)的左、右焦点分别为F1,F2,离心率e=
,过F1的直线交椭圆于M、N两点,且△MNF2周长为4
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)已知过椭圆中心,且斜率为k(k≠0)的直线与椭圆交于A、B两点,P是线段AB的垂直平分线与椭圆E的一个交点,若△APB的面积为
,求k的值.

| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 5 |
| 5 |
(Ⅰ)求椭圆E的方程;
(Ⅱ)已知过椭圆中心,且斜率为k(k≠0)的直线与椭圆交于A、B两点,P是线段AB的垂直平分线与椭圆E的一个交点,若△APB的面积为
| 40 |
| 9 |

(Ⅰ)∵△MNF2周长为4
,
∴4a=4
,
∴a=
,
∵离心率e=
,
∴c=1,
∴b=
=2,
∴椭圆E的方程为
+
=1;
(Ⅱ)直线AB的方程为y=kx,线段AB的垂直平分线为y=-
x,
y=-
x与椭圆方程联立,可得x=±
,
∴可得P(
,-
),
P到直线AB的距离为d=|
•
|
y=kx与椭圆方程联立,可得x=±
∴|AB|=
•2
∴S△ABP=
|AB|d|=
•2
•|
•
|
∵△APB的面积为
,
∴
•2
•|
•
|=
,
∴k4-2k2+1=0,
∴k=±1.
| 5 |
∴4a=4
| 5 |
∴a=
| 5 |
∵离心率e=
| ||
| 5 |
∴c=1,
∴b=
| a2-c2 |
∴椭圆E的方程为
| x2 |
| 5 |
| y2 |
| 4 |
(Ⅱ)直线AB的方程为y=kx,线段AB的垂直平分线为y=-
| 1 |
| k |
y=-
| 1 |
| k |
|
∴可得P(
|
| 1 |
| k |
|
P到直线AB的距离为d=|
| ||
| k |
|
y=kx与椭圆方程联立,可得x=±
|
∴|AB|=
| 1+k2 |
|
∴S△ABP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1+k2 |
|
| ||
| k |
|
∵△APB的面积为
| 40 |
| 9 |
∴
| 1 |
| 2 |
| 1+k2 |
|
| ||
| k |
|
| 40 |
| 9 |
∴k4-2k2+1=0,
∴k=±1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目