题目内容

已知抛物线C的顶点为O（0，0），焦点F（0，1）
（Ⅰ）求抛物线C的方程；
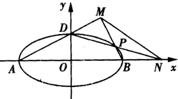
（Ⅱ）过F作直线交抛物线于A、B两点．若直线OA、OB分别交直线l：y=x-2于M、N两点，求|MN|的最小值．
（I）由题意可设抛物线C的方程为x2=2py（p＞0）则
p
2
=1，解得p=2，故抛物线C的方程为x2=4y
（II）设A（x1，y1），B（x2，y2），直线AB的方程为y=kx+1
由
y=kx+1
x2=4y
消去y，整理得x2-4kx-4=0
所以x1+x2=4k，x1x2=-4，从而有|x1-x2|=
(x1+x2)2-4x1x2
=4
k2+1

由
y=
y1
x1
x
y=x-2
解得点M的横坐标为xM=
2x1
x1-y1
=
2x1
x1-
x12
4
=
8
4-x1
，
同理可得点N的横坐标为xN=
8
4-x2

所以|MN|=
2
|xM-xN|=
2
|
8
4-x1
-
8
4-x2
|=8
2
|
x1-x2
x1x2-4(x1+x2)+16
|=
8
2
k2+1
|4k-3|

令4k-3=t，t不为0，则k=
t+3
4

当t＞0时，|MN|=2
2
25
t2
+
6
t
+1
＞2
2

当t＜0时，|MN|=2
2
25
t2
+
6
t
+1
=2
2
(
5
t
+
3
5
)2+
16
25
≥
8
2
5

综上所述，当t=-
25
3
时，|MN|的最小值是
8
2
5
练习册系列答案
相关题目
已知F是抛物线y2=4x上的焦点，P是抛物线上的一个动点，若动点M满足
FP
=2
FM
，则M的轨迹方程是______．
直线l：y=kx+1与双曲线C：3x2-y2=1相交于不同的A，B两点．
（1）求AB的长度；
（2）是否存在实数k，使得以线段AB为直径的圆经过坐标原点？若存在，求出k的值，若不存在，写出理由．
抛物线C：x2=2py（p＞0）的焦点为F，O为坐标原点；当抛物线上点N的纵坐标为1时，|NF|=2，已知直线l经过抛物线C的焦点F，且与抛物线C交于A，B两点
（1）求抛物线C的方程；
（2）若△AOB的面积为4，求直线l的方程．
已知点P（x0，y0）是椭圆C：
x2
5
+y2=1上的一点．F1、F2是椭圆C的左右焦点．
（1）若∠F1PF2是钝角，求点P横坐标x0的取值范围；
（2）求代数式
y20
+2x0的最大值．
已知椭圆
y2
a2
+
x2
b2
=1(a＞b＞0)的离心率e=
3
2
，短轴长为2，点A（x1，y1），B（x2，y2）是椭圆上的两点，
m
=(
x1
b
，
y1
a
)，
n
=(
x2
b
，
y2
a
)，且
m
•
n
=0．
（1）求椭圆方程；
（2）若直线AB过椭圆的焦点F（0，c）（c为半焦距），求直线AB的斜率；
（3）试问：△AOB的面积是否为定值？如果是，请给予证明；如果不是，请说明理由．
已知△ABC中，B（-2，0），C（2，0），△ABC的周长为12，动点A的轨迹为曲线E．
（1）求曲线E的方程；
（2）设P、Q为E上两点，
OP
•
OQ
=0，过原点O作直线PQ的垂线，垂足为M，证明|OM|为定值．
如图，在直角梯形ABCD中，AD∥BC，DA⊥AB，AD=3，AB=4，BC=
3
，点E在线段AB的延长线上．若曲线段DE（含两端点）为某曲线L上的一部分，且曲线L上任一点到A、B两点的距离之和都相等．
（1）建立恰当的直角坐标系，求曲线L的方程；
（2）根据曲线L的方程写出曲线段DE（含两端点）的方程；
（3）若点M为曲线段DE（含两端点）上的任一点，试求|MC|+|MA|的最小值，并求出取得最小值时点M的坐标．
椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率e=
3
2
，a+b=3．
（1）求椭圆C的方程；
（2）如图，A，B，D是椭圆C的顶点，P是椭圆C上除顶点外的任意点，直线DP交x轴于点N直线AD交BP于点M，设BP的斜率为k，MN的斜率为m，证明2m-k为定值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网