题目内容
6.已知函数f(x)=$\left\{\begin{array}{l}{x{\;}^{2},(x≤0)}\\{\sqrt{2-x{\;}^{2}},(x>0)}\end{array}\right.$则${∫}_{-1}^{\sqrt{2}}$f(x)dx=( )| A. | $\frac{π}{2}$-$\frac{1}{3}$ | B. | $\frac{π}{2}$+$\frac{1}{3}$ | C. | $\frac{π}{4}$+$\frac{1}{3}$ | D. | $\frac{π}{4}$-$\frac{1}{3}$ |
分析 由${∫}_{-1}^{\sqrt{2}}$f(x)dx=${∫}_{0}^{\sqrt{2}}$$\sqrt{2-{x}^{2}}$dx+${∫}_{-1}^{0}$x2dx,分别根据定积分的几何意义和定积分的计算法则计算计算即可.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{x{\;}^{2},(x≤0)}\\{\sqrt{2-x{\;}^{2}},(x>0)}\end{array}\right.$,
∴${∫}_{-1}^{\sqrt{2}}$f(x)dx=${∫}_{0}^{\sqrt{2}}$$\sqrt{2-{x}^{2}}$dx+${∫}_{-1}^{0}$x2dx,
∵${∫}_{0}^{\sqrt{2}}$$\sqrt{2-{x}^{2}}$dx表示以原点为圆心,以$\sqrt{2}$为半径的圆的面积的四分之一,
∴${∫}_{0}^{\sqrt{2}}$$\sqrt{2-{x}^{2}}$dx=$\frac{1}{4}$π•2=$\frac{π}{2}$,
∴${∫}_{-1}^{\sqrt{2}}$f(x)dx=${∫}_{0}^{\sqrt{2}}$$\sqrt{2-{x}^{2}}$dx+${∫}_{-1}^{0}$x2dx=$\frac{π}{2}$+$\frac{1}{3}$x3|${\;}_{-1}^{0}$=$\frac{π}{2}$+$\frac{1}{3}$,
故选:B.
点评 本题考查了定积分的计算和定积分的几何意义,属于中档题.

练习册系列答案
相关题目
1.点P(x0,y0)为椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1外一点,l:$\frac{{x}_{0}x}{4}$+$\frac{{y}_{0}y}{3}$=1,则l与C的关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 相交或相切 |
15.已知某天城市A下雨的概率为0.5,城市S下雨的概率为0.4,两城市同时下雨的概率为0,则两城市都没有下雨的概率为( )
| A. | 0.2 | B. | 0.5 | C. | 0.9 | D. | 0.1 |
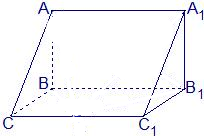 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BB1=2,BC=1,∠BCC1=$\frac{π}{3}$,且异面直线A1C于B1C1所成角的大小为arccos$\frac{\sqrt{10}}{5}$,求:
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BB1=2,BC=1,∠BCC1=$\frac{π}{3}$,且异面直线A1C于B1C1所成角的大小为arccos$\frac{\sqrt{10}}{5}$,求: