题目内容
16．曲线y=2x，y=2-x及直线x=-1，x=1所围成的图形的面积是$\frac{1}{ln2}$．分析 如图所示，利用对称性只要求出曲边△ABC的面积即可得出．S曲边△ABC=${∫}_{0}^{1}{2}^{x}dx$-${∫}_{0}^{1}（\frac{1}{2}）^{x}dx$，利用微积分基本定理即可得出．
解答 解：如图所示，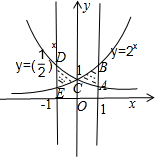
利用对称性只要求出曲边△ABC的面积即可得出．
S曲边△ABC=${∫}_{0}^{1}{2}^{x}dx$-${∫}_{0}^{1}（\frac{1}{2}）^{x}dx$
=$\frac{1}{ln2}$$[{2}^{x}{|}_{0}^{1}+（\frac{1}{2}）^{x}{|}_{0}^{1}]$
=$\frac{1}{2ln2}$．
故答案为：$\frac{1}{ln2}$．
点评 本题考查了微积分基本定理的应用，考查了推理能力与计算能力，属于中档题．
练习册系列答案
状元及第系列答案
同步奥数系列答案
相关题目
6．已知函数f（x）=$\left\{\begin{array}{l}{x{\;}^{2}，（x≤0）}\\{\sqrt{2-x{\;}^{2}}，（x＞0）}\end{array}\right.$则${∫}_{-1}^{\sqrt{2}}$f（x）dx=（ ）
| A． | $\frac{π}{2}$-$\frac{1}{3}$ | B． | $\frac{π}{2}$+$\frac{1}{3}$ | C． | $\frac{π}{4}$+$\frac{1}{3}$ | D． | $\frac{π}{4}$-$\frac{1}{3}$ |
7．设f（x）=a1x+a2x2+…+anxn（n为正整数），若f（1）=n2，则（ ）
| A． | an=2n-1，f（$\frac{1}{3}$）的最小值为1 | B． | an=n，f（$\frac{1}{3}$）的最小值为$\frac{1}{3}$ | ||
| C． | an=2n-1，f（$\frac{1}{3}$）的最小值为$\frac{1}{3}$ | D． | an=n，f（$\frac{1}{3}$）的最小值为$\frac{2}{3}$ |