Question

11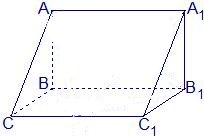．如图，在三棱柱ABC-A₁B₁C₁中，AB⊥侧面BB₁C₁C，已知BB₁=2，BC=1，∠BCC₁=$\frac{π}{3}$，且异面直线A₁C于B₁C₁所成角的大小为arccos$\frac{\sqrt{10}}{5}$，求：
（1）AB的长；
（2）三棱柱ABC-A₁B₁C₁的侧面积和体积．

Answer 1

分析 （1）△B₁BC中，利用余弦定理求得A₁C，设AB=x，解直角三角形求得A₁B，在△A₁BC中，利用余弦定理求得x的值；
（2）过B作CC₁的垂线BE，连接AE，则AE⊥CC₁，通过解直角三角形求得BE、AE的值，则三棱柱的侧面积可求，由三角形ABE的面积乘以BB₁的长度得三棱柱的体积．

解答 解：（1）如图，
∵AB⊥侧面BB₁C₁C，∴AB⊥BC，AB⊥BB₁，
∵∠BCC₁=$\frac{π}{3}$，∴∠$CB{B}_{1}=\frac{2π}{3}$，
在△B₁BC中，由BB₁=2，BC=1，∠CBB₁=$\frac{2π}{3}$，得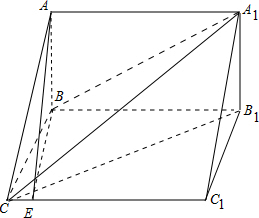
${B}_{1}{C}^{2}=B{C}^{2}+{B}_{1}{B}^{2}-2•BC•{B}_{1}B•cos∠CB{B}_{1}$=${1}^{2}+{2}^{2}-2×1×2cos\frac{2π}{3}=7$．
设AB=x，则${A}_{1}{C}^{2}={B}_{1}{C}^{2}+{A}_{1}{{B}_{1}}^{2}=7+{x}^{2}$，
${A}_{1}{B}^{2}={B}_{1}{B}^{2}+{A}_{1}{{B}_{1}}^{2}=4+{x}^{2}$，
在△A₁BC中，有${A}_{1}{B}^{2}={A}_{1}{C}^{2}+B{C}^{2}-2•{A}_{1}B•BC•cos（arccos\frac{\sqrt{10}}{5}）$，
∴$4+{x}^{2}=7+{x}^{2}+1-2\sqrt{7+{x}^{2}}×\frac{\sqrt{10}}{5}$，解得：x=$\sqrt{3}$．
∴AB的长为$\sqrt{3}$；
（2）过B作CC₁的垂线BE，连接AE，则AE⊥CC₁，
在Rt△BEC中，由BC=1，$∠BCE=\frac{π}{3}$，得BE=$\frac{\sqrt{3}}{2}$，∴$AE=\sqrt{（\sqrt{3}）^{2}+（\frac{\sqrt{3}}{2}）^{2}}=\frac{\sqrt{15}}{2}$．
∴三棱柱ABC-A₁B₁C₁的侧面积为$2×\sqrt{3}+2×\frac{\sqrt{3}}{2}+2×\frac{\sqrt{15}}{2}=3\sqrt{3}+\sqrt{15}$；
体积为V=$\frac{1}{2}×\sqrt{3}×\frac{\sqrt{3}}{2}×2=\frac{3}{2}$．

点评 本小题主要考查空间线面关系、异面直线所成角、几何体的体积等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力，是中档题．