题目内容
1．已知在锐角△ABC中，已知∠B=$\frac{π}{3}$，|$\overrightarrow{AB}$-$\overrightarrow{AC}$|=2，则$\overrightarrow{AB}•\overrightarrow{AC}$的取值范围是（0，12）．分析 以B为原点，BA所在直线为x轴建立坐标系，得到C的坐标，找出三角形为锐角三角形的A的位置，得到所求范围．
解答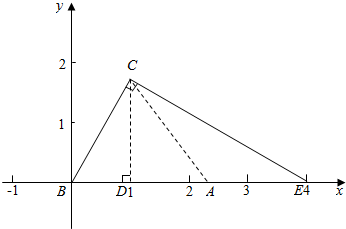 
解：以B为原点，BA所在直线为x轴建立坐标系，
因为∠B=$\frac{π}{3}$，|$\overrightarrow{AB}$-$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|=2，所以C（1，$\sqrt{3}$），设A（x，0）
因为△ABC是锐角三角形，所以A+C=120°，∴30°＜A＜90°，即A在如图的线段DE上（不与D，E重合），所以1＜x＜4，
则$\overrightarrow{AB}•\overrightarrow{AC}$=x2-x=（x-$\frac{1}{2}$）2-$\frac{1}{4}$，所以$\overrightarrow{AB}•\overrightarrow{AC}$的范围为（0，12）．
故答案为：（0，12）．
点评 本题考查了向量的几何意义以及利用坐标法求数量积范围；属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．若直线y=kx+3与直线y=$\frac{1}{k}$x-5的交点在直线y=x上，则k的值为（ ）
| A． | $\frac{3}{5}$ | B． | -$\frac{3}{5}$ | C． | -$\frac{5}{3}$ | D． | $\frac{5}{3}$ |
6．已知函数f（x）=$\left\{\begin{array}{l}{x{\;}^{2}，（x≤0）}\\{\sqrt{2-x{\;}^{2}}，（x＞0）}\end{array}\right.$则${∫}_{-1}^{\sqrt{2}}$f（x）dx=（ ）
| A． | $\frac{π}{2}$-$\frac{1}{3}$ | B． | $\frac{π}{2}$+$\frac{1}{3}$ | C． | $\frac{π}{4}$+$\frac{1}{3}$ | D． | $\frac{π}{4}$-$\frac{1}{3}$ |