题目内容
【题目】已知椭圆E: ![]() +
+ ![]() =1(a>b>0)的两个焦点为F1、F2 , 且椭圆E过点(0,
=1(a>b>0)的两个焦点为F1、F2 , 且椭圆E过点(0, ![]() ),(
),( ![]() ,﹣
,﹣ ![]() ),点A是椭圆上位于第一象限的一点,且△AF1F2的面积S△
),点A是椭圆上位于第一象限的一点,且△AF1F2的面积S△ ![]() =
= ![]() .
.
(1)求点A的坐标;
(2)过点B(3,0)的直线l与椭圆E相交于点P、Q,直线AP、AQ分别与x轴相交于点M、N,点C( ![]() ,0),证明:|CM||CN|为定值,并求出该定值.
,0),证明:|CM||CN|为定值,并求出该定值. 
【答案】
(1)解:由于椭圆E过点(0, ![]() ),(
),( ![]() ,﹣
,﹣ ![]() ),
),
∴ 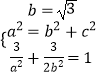 ,解得b=c=
,解得b=c= ![]() ,a2=6,
,a2=6,
∴椭圆E的方程为: ![]() .
.
∵△AF1F2的面积S△AF1F2= ![]() .
.
∴ ![]() =
= ![]() ,
,
∴yA=1,代入椭圆方程可得: ![]() ,
,
∵xA>0,解得xA=2.
∴A(2,1).
(2)证明:设直线l的方程为:my=x﹣3,P(x1,y1),Q(x2,y2).
直线AP的方程为:y﹣1= ![]() (x﹣2),可得M
(x﹣2),可得M ![]() ,即M
,即M ![]() .
.
直线AQ的方程为:y﹣1= ![]() (x﹣2),可得N
(x﹣2),可得N ![]() ,即N
,即N ![]() .
.
联立 ![]() ,化为:(2+m2)y2+6my+3=0.
,化为:(2+m2)y2+6my+3=0.
△>0,可得m2>1.
∴y1+y2= ![]() ,
, ![]() .
.
∴|CM||CN|= ![]()
![]() =
= ![]()
= ![]()
=  =
= ![]() =
= ![]() ,为定值.
,为定值.
【解析】(1)由于椭圆E过点(0, ![]() ),(
),( ![]() ,﹣
,﹣ ![]() ),联立
),联立 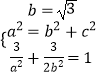 ,可得椭圆的方程.由于△AF1F2的面积S△AF1F2=
,可得椭圆的方程.由于△AF1F2的面积S△AF1F2= ![]() ,利用
,利用 ![]() =
= ![]() ,可得yA=1,代入椭圆方程可得得xA . 即可得出A的坐标.(2)设直线l的方程为:my=x﹣3,P(x1 , y1),Q(x2 , y2).直线AP的方程为:y﹣1=
,可得yA=1,代入椭圆方程可得得xA . 即可得出A的坐标.(2)设直线l的方程为:my=x﹣3,P(x1 , y1),Q(x2 , y2).直线AP的方程为:y﹣1= ![]() (x﹣2),M
(x﹣2),M ![]() .同理可得N
.同理可得N ![]() .联立
.联立 ![]() ,化为:(2+m2)y2+6my+3=0.利用根与系数的关系可得y1+y2 , y1y2 . 即可证明|CM||CN|为定值.
,化为:(2+m2)y2+6my+3=0.利用根与系数的关系可得y1+y2 , y1y2 . 即可证明|CM||CN|为定值.

 作业辅导系列答案
作业辅导系列答案

