题目内容
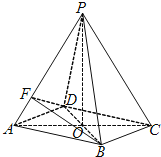
【题目】如图1，直角梯形ABCD中，∠ABC=90°，AB=BC=2AD=4，点E、F分别是AB、CD的中点，点G在EF上，沿EF将梯形ABCD翻折，使平面AEFD⊥平面EBCF，如图2．
（1）当AG+GC最小时，求证：BD⊥CG；
（2）当2VB﹣ADGE=VD﹣GBCF时，求二面角D﹣BG﹣C平面角的余弦值．
【答案】
（1）
证明：∵点E、F分别是AB、CD的中点，
∴EF∥BC，又∠ABC=90°，∴AE⊥EF，
∵平面AEFD⊥平面EBCF，
∴AE⊥平面EBCF，AE⊥EF，AE⊥BE，又BE⊥EF，
如图建立空间坐标系E﹣xyz．
翻折前，连结AC交EF于点G，此时点G使得AG+GC最小．
EG= 
BC=2，又∵EA=EB=2．
则A（0，0，2），B（2，0，0），C（2，4，0），
D（0，2，2），E（0，0，0），G（0，2，0），
∴ 
=（﹣2，2，2）， 
=（﹣2，﹣2，0）
∴ 
=（﹣2，2，2）（﹣2，﹣2，0）=0，
∴BD⊥CG．
（2）
解法一：设EG=k，∵AD∥平面EFCB，
∴点D到平面EFCB的距离为即为点A到平面EFCB的距离．
∵ 
[（3﹣k）+4]×2=7﹣k，
∴ 
= 
，
又 
= 
，
∵2VB﹣ADGE=VD﹣GBCF，∴ 
= ，
∴k=1即EG=1
设平面DBG的法向量为 
，∵G（0，1，0），
∴ 
， =（﹣2，2，2），
则 
，即 
取x=1，则y=2，z=﹣1，∴ 
面BCG的一个法向量为 
则cos＜ 
＞= 
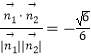
由于所求二面角D﹣BF﹣C的平面角为锐角，
所以此二面角平面角的余弦值为 
解法二：由解法一得EG=1，过点D作DH⊥EF，垂足H，
过点H作BG延长线的垂线垂足O，连接OD．
∵平面AEFD⊥平面EBCF，
∴DH⊥平面EBCF，∴OD⊥OB，
∴∠DOH就是所求的二面角D﹣BG﹣C的平面角．
由于HG=1，在△OHG中 
，
又DH=2，在△DOH中 
∴此二面角平面角的余弦值为 ．
【解析】（1）由已知条件推导出AE⊥EF，AE⊥BE，BE⊥EF，建立空间坐标系E﹣xyz，利用向量法能求出BD⊥CG．（2）法一：设EG=k，由AD∥平面EFCB，得到点D到平面EFCB的距离为即为点A到平面EFCB的距离．分别求出平面DBG的法向量和面BCG的一个法向量，利用向量法能求出二面角平面角的余弦值．法二：由已知条件指法训练出EG=1，过点D作DH⊥EF，垂足H，过点H作BG延长线的垂线垂足O，连接OD．由已知条件推导出∠DOH就是所求的二面角D﹣BG﹣C的平面角，由此能求出此二面角平面角的余弦值．
【考点精析】掌握平面与平面垂直的性质是解答本题的根本，需要知道两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直．
