题目内容
【题目】已知点![]() ,圆
,圆![]() ,点
,点![]() 在圆
在圆![]() 上运动.
上运动.
(![]() )如果
)如果![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
(![]() )如果直线
)如果直线![]() 与圆
与圆![]() 的另一个交点为
的另一个交点为![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)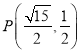 或
或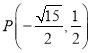 ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)设点![]() ,所以
,所以![]() ,由
,由![]() 是等腰三角形,得
是等腰三角形,得![]() 或
或![]() ,分别列方程组求解即可;
,分别列方程组求解即可;
(2)易知直线![]() 为
为![]() 轴时不合题意,由此可设直线
轴时不合题意,由此可设直线![]() 方程为
方程为![]() ,与圆联立可得
,与圆联立可得![]() ,由
,由![]() ,用坐标表示,结合韦达定理求解即可.
,用坐标表示,结合韦达定理求解即可.
试题解析:
(![]() )因为圆
)因为圆![]() ,
,
所以![]() ,半径为
,半径为![]() .
.
设点![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() ,
, ![]() ,
,
因为![]() 是等腰三角形,
是等腰三角形,
所以![]() 或
或![]() .
.
当![]() 时,有
时,有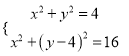 ,
,
解得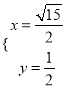 或
或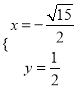 ,
,
所以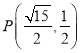 或
或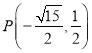 .
.
当![]() 时,有
时,有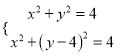 ,
,
解得![]() ,此时
,此时![]() ,
, ![]() ,
, ![]() 三点共线,不合题意.
三点共线,不合题意.
综上, 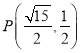 或
或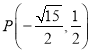 .
.
(![]() )若直线
)若直线![]() 为
为![]() 轴,则
轴,则![]() ,
, ![]() 或
或![]() ,
, ![]() .
.
而![]() ,不合题意.
,不合题意.
由此可设直线![]() 方程为
方程为![]() ,
,
设![]() ,
, ![]() ,
,
由![]() 得
得![]() ,
,
其中![]() ,
,
且![]() ,
, ![]() ,
,
因为![]() ,
,
所以![]() ,
, ![]() ,
,
又因为![]() ,
,
所以![]() ,
,
将![]() ,
, ![]() 代入上式,
代入上式,
整理得![]() ,
,
所以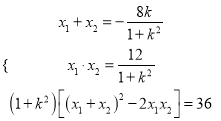 ,
,
解得![]() ,即
,即![]() ,经检验符合题意,
,经检验符合题意,
所以![]() 或
或![]() .
.

练习册系列答案
相关题目



