题目内容
11.在(2$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)6的展开式中,含x2项的系数是-192.分析 写出二项展开式的通项,由x的次数为2求得r值,则含x2项的系数可求.
解答 解:∵${T}_{r+1}={C}_{6}^{r}(2\sqrt{x})^{6-r}•(-\frac{1}{\sqrt{x}})^{r}$=$(-1)^{r}{C}_{6}^{r}•{2}^{6-r}•{x}^{3-r}$,
由3-r=2,得r=1.
∴含x2项的系数是-${C}_{6}^{1}$×25=-192.
故答案为:-192.
点评 本题考查了二项式系数的性质,关键是对二项展开式通项的记忆与运用,是基础题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
1.“x>1”是“︳x|>1”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分又不必要 |
2.在如图所示的四个图示中,是结构图的是( )
| A. | 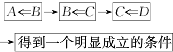 | B. | 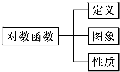 | ||
| C. | 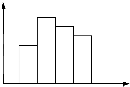 | D. | 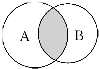 |
6.“$\frac{1}{a}$>1”是“函数f(x)=(3-2a)x单调递增”( )
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充分且必要 | D. | 既不充分也不必要 |
3.b,c表示两条不重合的直线,α,β表示两个不重合的平面,下列命题中正确的是( )
| A. | $\left.\begin{array}{l}{c∥α}\\{b?α}\end{array}\right\}$⇒c∥b | B. | $\left.\begin{array}{l}{c∥α}\\{α⊥β}\end{array}\right\}$⇒c⊥β | C. | $\left.\begin{array}{l}{c⊥α}\\{c⊥β}\end{array}\right\}$⇒α∥β | D. | $\left.\begin{array}{l}{b∥c}\\{c?α}\end{array}\right\}$⇒b∥α |
1.设复数z1=-1+i,z2=$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i,则$\frac{{z}_{1}}{{z}_{2}}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |