题目内容
数列{an}中,已知对任意n∈N*,a1+a2+a3+…+an=3n-1,则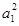 +
+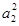 +
+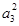 +…+
+…+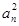 等于( )
等于( )
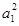 +
+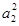 +
+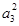 +…+
+…+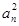 等于( )
等于( )| A.(3n-1)2 | B.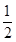 (9n-1) (9n-1) |
| C.9n-1 | D.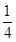 (3n-1) (3n-1) |
B
已知a1+a2+a3+…+an=3n-1,①
当n≥2时,a1+a2+…+an-1=3n-1-1,②
由①-②得an=(3n-1)-(3n-1-1)=2·3n-1,
∴{an}是首项为2,公比为3的等比数列.
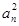 =(2·3n-1)2=4·32n-2=4·9n-1,
=(2·3n-1)2=4·32n-2=4·9n-1,
∴{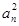 }是首项为4,公比为9的等比数列,
}是首项为4,公比为9的等比数列,
故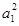 +
+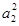 +…+
+…+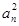 =
= =
=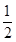 (9n-1).
(9n-1).
当n≥2时,a1+a2+…+an-1=3n-1-1,②
由①-②得an=(3n-1)-(3n-1-1)=2·3n-1,
∴{an}是首项为2,公比为3的等比数列.
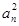 =(2·3n-1)2=4·32n-2=4·9n-1,
=(2·3n-1)2=4·32n-2=4·9n-1,∴{
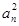 }是首项为4,公比为9的等比数列,
}是首项为4,公比为9的等比数列,故
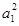 +
+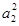 +…+
+…+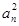 =
= =
=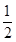 (9n-1).
(9n-1).
练习册系列答案
相关题目
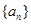 ,其前
,其前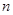 项和
项和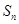 满足
满足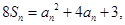 且
且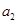 是
是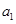 和
和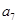 的等比中项.
的等比中项.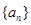 的通项公式;
的通项公式;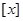 表示不超过实数
表示不超过实数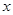 的最大整数,记
的最大整数,记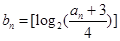 ,求
,求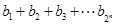 .
.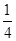 ,则a1a2+a2a3+…+anan+1(n∈N*)的取值范围是________.
,则a1a2+a2a3+…+anan+1(n∈N*)的取值范围是________.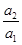 ,
,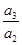 ,…,
,…,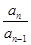 ,…是首项为1,公比为-
,…是首项为1,公比为- 的等比数列,那么a5等于( )
的等比数列,那么a5等于( )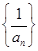 的前5项和为( )
的前5项和为( )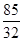
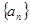 是递增数列,
是递增数列,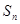 是
是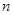 项和.若
项和.若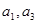 是方程
是方程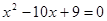 的两个根,则
的两个根,则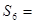 _________ .
_________ .