题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,过
,过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点.
两点.
(1)若以![]() 为直径的动圆内切于圆
为直径的动圆内切于圆![]() ,求椭圆的长轴长;
,求椭圆的长轴长;
(2)当![]() 时,问在
时,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?并说明理由.
为定值?并说明理由.
【答案】(Ⅰ)6(Ⅱ)见解析
【解析】试题分析:(1)设![]() 的中点为
的中点为![]() ,可得
,可得![]() ,当两个圆相内切时 ,两个圆的圆心距等于两个圆的半径差,即
,当两个圆相内切时 ,两个圆的圆心距等于两个圆的半径差,即![]() ,所以
,所以![]() ,椭圆长轴长为
,椭圆长轴长为![]() ;(2)先求得椭圆方程为
;(2)先求得椭圆方程为![]() , 设直线AB方程为:
, 设直线AB方程为:![]() ,联立可得
,联立可得![]() ,设
,设![]() 根据韦达定理及平面向量数量积公式可得
根据韦达定理及平面向量数量积公式可得![]() ,当
,当![]() 即
即![]() 时
时![]() 为定值.
为定值.
试题解析:(Ⅰ)设![]() 的中点为M,在三角形
的中点为M,在三角形![]() 中,由中位线得:
中,由中位线得:
![]()
当两个圆相内切时 ,两个圆的圆心距等于两个圆的半径差,即![]()
所以![]() ,椭圆长轴长为6.
,椭圆长轴长为6.
(Ⅱ)由已知![]() ,
,![]()
![]() ,所以椭圆方程为
,所以椭圆方程为![]()
当直线AB斜率存在时,设直线AB方程为:![]()
设![]()
由![]() 得
得![]()
![]() 恒成立
恒成立
![]()
![]()
![]()
设![]()
![]()
![]()
当![]() 即
即![]() 时
时![]() 为定值
为定值![]()
当直线AB斜率不存在时,不妨设![]()
当![]() 时
时![]() ,为定值
,为定值
综上:在X轴上存在定点![]() ,使得
,使得![]() 为定值
为定值![]()

练习册系列答案
相关题目
【题目】某动漫影视制作公司长期坚持文化自信,不断挖掘中华优秀传统文化中的动漫题材,创作出一批又一批的优秀动漫影视作品,获得市场和广大观众的一致好评.同时也为公司赢得丰厚的利润,该公司2013年至2019年的年利润![]() 关于年份代号
关于年份代号![]() 的统计数据如下表(已知该公司的年利润与年份代号线性相关)
的统计数据如下表(已知该公司的年利润与年份代号线性相关)
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
年利润 | 29 | 33 | 36 | 44 | 48 | 52 | 59 |
(1)求![]() 关于
关于![]() 的线性回归方程,并预测该公司2020年的年利润;
的线性回归方程,并预测该公司2020年的年利润;
(2)当统计表中某年年利润的实际值大于由(1)中线性回归方程计算出该年利润的估计值时,称该年为A级利润年,否则称为B级利润年.现从2015年至2019年这5年中随机抽取2年,求恰有1年为A级利润年的概率.
参考公式: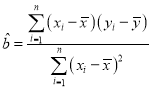 ,
,![]()