题目内容
【题目】(1)解不等式:![]() ;
;
(2)已知a-5x>ax+7(a>0,且a≠1),求x的取值范围.
【答案】(1){x|x≥0}.
(2)当a>1时,x<-![]() ;当0<a<1时,x>-
;当0<a<1时,x>-![]() .
.
【解析】
(1)根据指数函数的单调性可将原不等式化为![]() ,从而可得结果;(2)分两种情况讨论,分别利用指数函数的单调性,化简原不等式求解即可.
,从而可得结果;(2)分两种情况讨论,分别利用指数函数的单调性,化简原不等式求解即可.
(1)因为![]() ,
,
所以原不等式可以转化为![]()
因为y=![]()
![]() 在R上是减函数,
在R上是减函数,
所以3x-1≥-1,所以x≥0.
故原不等式的解集是{x|x≥0}.
(2)当a>1时,因为a-5x>ax+7,所以-5x>x+7,
解得x<-![]() ;
;
当0<a<1时,因为a-5x>ax+7,所以-5x<x+7,
解得x>-![]() .
.
综上所述,x的取值范围是:当a>1时,x<-![]() ;
;
当0<a<1时,x>-![]() .
.

【题目】某单位鼓励员工参加健身运动,推广了一款手机软件,记录每人每天走路消耗的卡路里;软件的测评人员从员工中随机地选取了40人(男女各20人),记录他们某一天消耗的卡路里,并将数据整理如下:
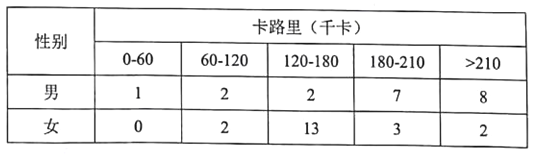
(1)已知某人一天的走路消耗卡路里超过180千卡被评测为“积极型”,否则为“懈怠型”,根据题中数据完成下面的![]() 列联表,并据此判断能否有99%以上把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有99%以上把握认为“评定类型”与“性别”有关?
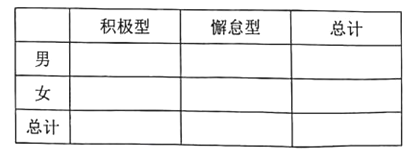
(2)若测评人员以这40位员工每日走路所消耗的卡路里的频率分布来估计其所有员工每日走路消耗卡路里的频率分布,现在测评人员从所有员工中任选2人,其中每日走路消耗卡路里不超过120千卡的有![]() 人,超过210千卡的有
人,超过210千卡的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: 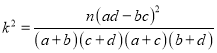 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【题目】哈三中群力校区高二、六班同学用随机抽样的办法对所在校区老师的饮食习惯进行了一次调查, 饮食指数结果用茎叶图表示如图, 图中饮食指数低于70的人是饮食以蔬菜为主;饮食指数高于70的人是饮食以肉类为主.

(1)完成下列2×2列联表:

能否有99%的把握认为老师的饮食习惯与年龄有关?
(2)从群力校区任选一名老师, 设“选到45岁以上老师”为事件![]() , “饮食指数高于70的老师”为事件
, “饮食指数高于70的老师”为事件![]() , 用调查的结果估计
, 用调查的结果估计![]() 及
及![]() (用最简分数作答);
(用最简分数作答);
(3)为了给食堂提供老师的饮食信息, 根据(1)(2)的结论,能否有更好的抽样方法来估计老师的饮食习惯, 并说明理由.附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()