Question

【题目】已知函数f（x）=（ ）x ， g（x）=x2 ， 对于不相等的实数x1 ， x2 ， 设m= ，n= ，则下列说法正确的有（ ）
①对于任意不相等的实数x1 ， x2 ， 都有m＜0；
②对于任意不相等的实数x1 ， x2 ， 都有n＜0；
③存在不相等的实数x1 ， x2 ， 使得m=n．
A.①
B.①③
C.②③
D.①②③

Answer 1

【答案】B
【解析】解：分别画出函数f（x），g（x）的图象，
则m= 表示曲线f（x）上两点的斜率，n= 表示曲线g（x）上两点的斜率，
由图象可知，①对于任意不相等的实数x1 ， x2 ， 都有m＜0，故①正确，
对于任意不相等的实数x1 ， x2 ， 都有n＞0或n＜0，故②错误，
存在不相等的实数x1 ， x2 ， 使得m=n，故③正确，
故选：B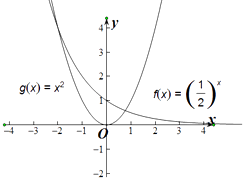

【考点精析】关于本题考查的函数单调性的性质，需要了解函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集才能得出正确答案．