Question

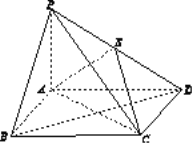
【题目】在直三棱柱ABC－A1B1C1中，AB＝AC，E是BC的中点，求证：

（Ⅰ）平面AB1E⊥平面B1BCC1；

（Ⅱ）A1C//平面AB1E．

Answer 1

【答案】（1）见解析（2）见解析

【解析】试题分析：（1）先根据直棱柱的性质，可得平面，可得，再根据等腰三角形性质可得，从而可得平面，进而得出结果；（2）连接，设，连接，由平行四边形的性质结合中位线定理可得.根据线面平行的判定定理可得结果.

试题解析：（1）在直三棱柱ABC－A1B1C1中，CC1平面ABC．

因为AE平面ABC，

所以CC1AE．

因为AB＝AC，E为BC的中点，所以AEBC．

因为BC在平面B1BCC1，内，CC1在平面B1BCC1内

且BC∩CC1＝C，

所以AE平面B1BCC1．

因为AE在平面AB1E内

所以平面AB1E平面B1BCC1.

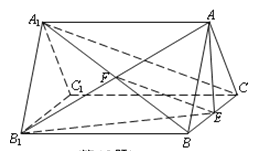
（2）连接A1B，设A1B∩AB1＝F，连接EF．

在直三棱柱ABC－A1B1C1中，四边形AA1B1B为平行四边形，

所以F为A1B的中点．

又因为E是BC的中点，所以EF∥A1C．

因为EF在平面AB1E内，A1C不在平面AB1E内，

所以A1C∥平面AB1E.

【方法点晴】本题主要考查线面平行的判定定理以及线面垂直、面面垂直的判定，属于难题.证明线面平行的常用方法：①利用线面平行的判定定理，使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线，可利用几何体的特征，合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质，即两平面平行，在其中一平面内的直线平行于另一平面. 本题（2）是就是利用方法①证明的.