题目内容
【题目】已知命题p:设a,b∈R,则“a+b>4”是“a>2且b>2”的必要不充分条件;命题q:若 ![]() <0,则
<0,则 ![]() ,
, ![]() 夹角为钝角,在命题①p∧q;②¬p∨¬q;③p∨¬q;④¬p∨q中,真命题是( )
夹角为钝角,在命题①p∧q;②¬p∨¬q;③p∨¬q;④¬p∨q中,真命题是( )
A.①③
B.①④
C.②③
D.②④
【答案】C
【解析】解:当a=1,b=5时,满足a+b>4,但a>2且b>2不成立, 若a>2且b>2,则a+b>4成立,则“a+b>4”是“a>2且b>2”的必要不充分条件,
故命题p为真命题.
当 ![]() ,
, ![]() 夹角θ=π时,满足
夹角θ=π时,满足 ![]() =|
=| ![]() ||
|| ![]() |cosπ=﹣|
|cosπ=﹣| ![]() ||
|| ![]() |<0,但
|<0,但 ![]() ,
, ![]() 夹角为钝角不成立,
夹角为钝角不成立,
故命题q为假命题.
则①p∧q为假命题.;②¬p∨¬q为真命题.;③p∨¬q为真命题.;④¬p∨q为假命题.
故真命题的是②③,
故选:C
【考点精析】关于本题考查的复合命题的真假,需要了解“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真才能得出正确答案.

练习册系列答案
相关题目
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg)其频率分布直方图如下:
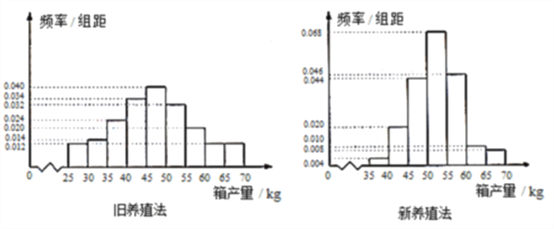
(1) 记![]() 表示事件“旧养殖法的箱产量低于50kg”,估计
表示事件“旧养殖法的箱产量低于50kg”,估计![]() 的概率;
的概率;
(2)填写下面联表,并根据列联表判断是否有![]() %的把握认为箱产量与养殖方法有关:
%的把握认为箱产量与养殖方法有关:
箱产量 | 箱产量 | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对两种养殖方法的优劣进行比较.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |