题目内容
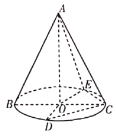
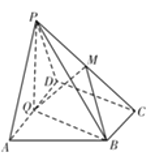
【题目】如图,在直角梯形![]() 中,
中,![]() ,平面
,平面![]() 外一点
外一点![]() 在平
在平![]() 内的射影
内的射影![]() 恰在边
恰在边![]() 的中点
的中点![]() 上,
上,![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 在线段
在线段![]() 上,且
上,且![]() 平面
平面![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)推导出PQ⊥平面ABCD,PQ⊥AD,CD∥BQ,从而BQ⊥AD,进而AD⊥平面PBQ,由此能证明平面PQB⊥平面PAD.
(2)连接AC与BQ交于点N,则N为AC中点,则点M到平面PAB的距离是点C到平面PAB的距离的![]() ,求出三棱锥P-ABC的体积V=
,求出三棱锥P-ABC的体积V=![]() ,PAB的面积为
,PAB的面积为![]() ,设点M到平面PAB的距离为d,由VC-PAB=VP-ABC,能求出点M到平面PAB的距离.
,设点M到平面PAB的距离为d,由VC-PAB=VP-ABC,能求出点M到平面PAB的距离.
(1)∵P在平面ABCD内的射影Q恰在边AD上,
∴PQ⊥平面ABCD,
∵AD平面ABCD,∴PQ⊥AD,
∵Q为线段AD中点,
∴CD∥BQ,∴BQ⊥AD,∴AD⊥平面PBQ,AD平面PAD,
∴平面PQB⊥平面PAD.
(2)连接AC与BQ交于点N,则N为AC中点,

∴点M到平面PAB的距离是点C到平面PAB的距离的![]() ,
,
在三棱锥P-ABC中,高PQ=![]() ,底面积为
,底面积为![]() ,
,
∴三棱锥P-ABC的体积V=![]() =
=![]() ,
,
又△PAB中,PA=AB=2,PB=![]() ,
,
∴△PAB的面积为![]() ,
,
设点M到平面PAB的距离为d,
由VC-PAB=VP-ABC,得![]() =
=![]() ,
,
解得d=![]() ,
,
∴点M到平面PAB的距离为![]() .
.

【题目】某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,统计结果如下表所示,已知这100位顾客中一次购物量超过7件的顾客占![]() .
.
一次购物量 | 1至3件 | 4至7件 | 8至11件 | 12至15件 | 16件及以上 |
顾客数(人) |
| 27 | 20 |
| 10 |
结算时间( | 0.5 | 1 | 1.5 | 2 | 2.5 |
(1)确定![]() ,
,![]() 的值,并求顾客一次购物的结算时间的平均值;
的值,并求顾客一次购物的结算时间的平均值;
(2)从收集的结算时间不超过![]() 的顾客中,按分层抽样的方法抽取5人,再从这5人中随机抽取2人,求至少有1人的结算时间为
的顾客中,按分层抽样的方法抽取5人,再从这5人中随机抽取2人,求至少有1人的结算时间为![]() 的概率.(注:将频率视为概率)
的概率.(注:将频率视为概率)